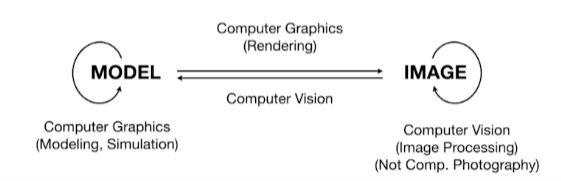
# Overview of Computer Graphics

最困难的特效是日常的效果。

需要猜测的是计算机视觉 (CV).

从 Model 到 Image：计算机图形学。
从 Image 到 Model：计算机视觉。

# Review of Linear Algebra

# Transformation

变换包括模型变换 (Modeling) 和视图变换 (Viewing).

三维到二维：投影 (Projecting).

# 基本几何变换

# 缩放变换

$$x' = s_xx \quad y' = s_yy$$

表示成矩阵形式为

$$\left(\begin{matrix} x' \\ y' \end{matrix}\right) = \left(\begin{matrix} s_x & 0 \\ 0 & s_y \end{matrix}\right) \left(\begin{matrix} x \\ y \end{matrix}\right)$$

对称变换类似，缩放系数变为$-1$ 即可。

# 切变

Shear Matrix

矩形变成平行四边形

$$x' = x + ay \quad y' = y$$

即

$$\left(\begin{matrix} x' \\ y' \end{matrix}\right) = \left(\begin{matrix} 1 & a \\ 0 & 1 \end{matrix}\right) \left(\begin{matrix} x \\ y \end{matrix}\right)$$

只需要变换前后的$x$、$y$ 关系.

# 旋转

表示绕原点逆时针旋转$\theta$ 的旋转矩阵为

$$R_\theta = \left(\begin{matrix} \cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{matrix}\right)$$

# 齐次坐标

平移不能写成矩阵乘法形式。只能写成

$$\left(\begin{matrix} x' \\ y' \end{matrix}\right) = \left(\begin{matrix} a & b \\ c & d \end{matrix}\right) \left(\begin{matrix} x \\ y \end{matrix}\right) + \left(\begin{matrix} t_x \\ t_y \end{matrix}\right)$$

于是出现齐次坐标的概念。点坐标写作$(x,y,1)'$, 向量坐标写作$(x,y,0)'$. 仿射变换都可以写成齐次坐标的线性变换。矩阵形式为：

$$\left(\begin{matrix} x' \\ y' \\ 1 \end{matrix}\right) = \left(\begin{matrix} a & b & t_x \\ c & d & t_y \\ 0 & 0 & 1 \end{matrix}\right) \left(\begin{matrix} x \\ y \\ 1 \end{matrix}\right)$$

代价是矩阵升高了一维。

# 光栅化

# 视口变换

不改变$z$ 的位置。将$x,y$ 轴变换到屏幕的像素点位置。

$$\left(\begin{matrix} \frac{width}{2} & 0 & 0 & \frac{width}{2} \\ 0 & \frac{height}{2} & 0 & \frac{height}{2} \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{matrix}\right)$$

隔行扫描：减少工作量，至今在视频压缩中仍然有用。但会造成严重的画面撕裂。

# 成像设备

LCD 液晶显示器

LED 发光二极管

Electrophoretic Display 电子墨水屏：刷新率很低。

# 三角形

基本的凸图形，内外易表示，渐变易计算。光栅化最重要的是判断像素中心点与三角形的位置关系。

# 采样