# 概述

文章标题 Resource-Aware Adaptive Indexing for In-situ Visual Exploration and Analytics 含义为：基于资源感知自适应索引方式的现场数据可视化探索与分析。

# 背景

文章希望为数据分析这提供生数据的快速分析方式。有如下要求：

数据是基于地图显示的 (关于地理位置的数据)
- 数据需要借助 2D 地图展示
- 地图需要便利地进行缩放、滑动
需要进行范围内的统计量、聚合函数计算 / 过滤等数据库查找
数据量大
在线查询

# 主要贡献

其主要贡献在于：

一种通过在主存内生数据上建立混合索引的方式
基于分类属性，标准化探索和分析数据的操作，并将操作关联至索引模式
一种基于交互信息增量更新索引数据的方法
基于资源感知的索引初始化方式（应用于内存有限的硬件）
将资源感知的初始化方式转化为一个优化问题，并证明优化问题是 NP-hard 的，同时提出了两种该 NP-hard 问题的近似算法

# 基本记号

符号	含义
\mathcal{O}=\	对象集 (set of Objects) 和其中的对象 (Object)
$A_i$	属性 (Attribute)
$h$	一个 CET 层次结构 (Hierarchy)
h.\mathcal	CET $h$ 中包含的对象集
$h.\mathcal{C} = \{A_{C_1},A_{C_2},\dots,A_{C_k}\}$	属性集（和其中的属性）
$\\|\mathcal{C}\\|$	$\mathcal{C}$ 的中的属性数，如果 $\mathcal{C}$ 隶属于一个 CET, 那么该 CET 的高度为 $\\|\mathcal{C}\\|+1$
$\mathrm{dom}(A_{C_i})$	属性 $A_{C_i}$ 取值的域
$n$	某个 CET 的一个节点 (Node)
$n.S = \langle v_0,v_1,\dots,v_k\rangle$	某个节点对应的有序属性值列，从 CET 的根节点开始
n.\mathcal	节点 $n$ 所对应的对象集
$t$	一个方片 (tile)
$t.I_x$	$t$ 在属性 $A_x$ 下所占据的范围
$\mathbb{I} = \langle\mathbb{I_\mathcal{T}}, \text{IT}, \text{IH}, \text{AS}\rangle$	一个 VETI 索引 (Index)
\mathbb{I}_\mathcal	$\mathbb{I}$ 所对于的方片集 (tiles)
\text	tile 的初始化策略 (tiles initialization strategy)
\text	树的初始化策略 (tree initialization strategy)
\text	基于用户交互重新构造 tile 和 CET 的方法 (adaptation strategy)

# CET-tree

CET - 树 (Categorical Exploration Tree, CET) 是作者提出的一种轻量级的，面向内存的，基于分类属性 (categorical attribute) 组织对象的树形数据结构。与字典树 (trie) 类似。

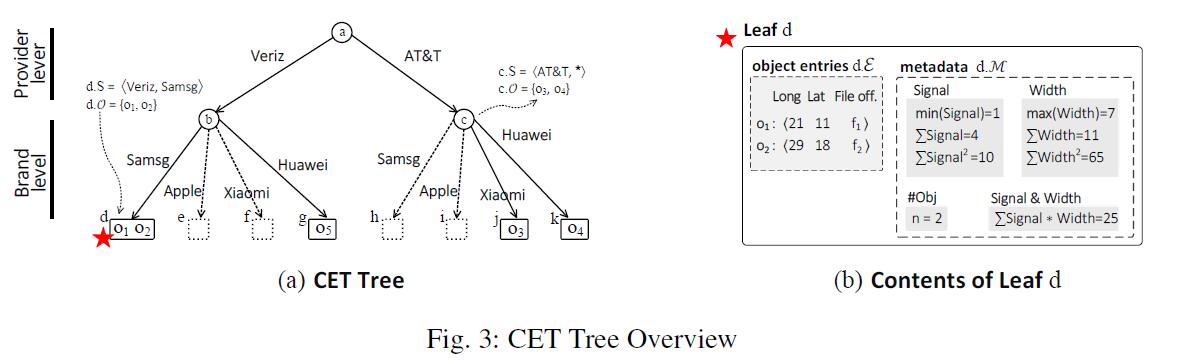
# 挑战

CET 设计的挑战包括：

高效的内存使用
降低 I/O 操作

符号系统是什么一摊狗屎 *

# 操作和复杂度分析

# 插入对象

按层高进行遍历，插入到叶子节点。复杂度 $O(|\mathcal{C}|)$ . 类似地，建树的复杂度为 $O(|\mathcal{O}|\cdot|\mathcal{C}|)$ .

# 基于过滤获取子对象

文中给出的复杂度是基于枚举的 $O(|\mathcal{O}|+N)$ . $N$ 是 CET 中的节点数。

极其容易改进吧。思路包括：

属性排序 + 二分查找
每层变成一个 hash 表

# 添加新属性

显然树的高度会 ++，于是最坏复杂度是 $O(|O|)$ . 写个 $O(|\mathcal{O}|\cdot |\mathcal{C}|)$ 什么鬼？

# 树的空间复杂度

最大节点数为

$1+\sum_{i=1}^k\prod_{j=1}^i|\mathrm{dom}(A_{C_i})| \;( \approx O(\mathcal{O}))$

递归与否差不多，主要看如何表述。

文章还给了一个基本假设：所有节点的内存占用基本相同？？？

一定不相同吧，不然就可以优化。

所以文章最后给出的空间复杂度是

$O\left(\alpha\sum_{i=0}^{|C|}\varGamma_i+\beta\cdot|\mathcal{O}|\right)$

其中 $\alpha$ 是一个节点的内存占用， $\beta$ 是一个对象的内存占用， $\varGamma_i$ 是树的第 $i$ 层的节点数目，满足 $1=\varGamma_0 \leq \varGamma_1 \leq\cdots\leq\varGamma_{|\mathcal{C}|}\leq|\mathcal{O}|$ .

# 按属性顺序建树

作者单独提到的，仅使得内存消耗降低 $10\%$ .

# 总结

文章只给出了最基本的 CET 操作，换句话说，CET 操作有扩展的可能性
CET 可加入 cache, 索引等进行加速

# VETI

VETI 是作者提出的一种索引方案，称为可视化探索的方片树索引 (Visual Exploration Tile-Tree Index, VETI). VETI 包括 tile 结构和 CET.

# tiles

方片结构 (tile structure) 是 VETI 的重要组成部分。可以看作一个二维的 data cube (而不是 Treemap).
Tile 结构有如下特点：

本身是层次结构
在每一个层次结构上，tile 都是不重叠的。

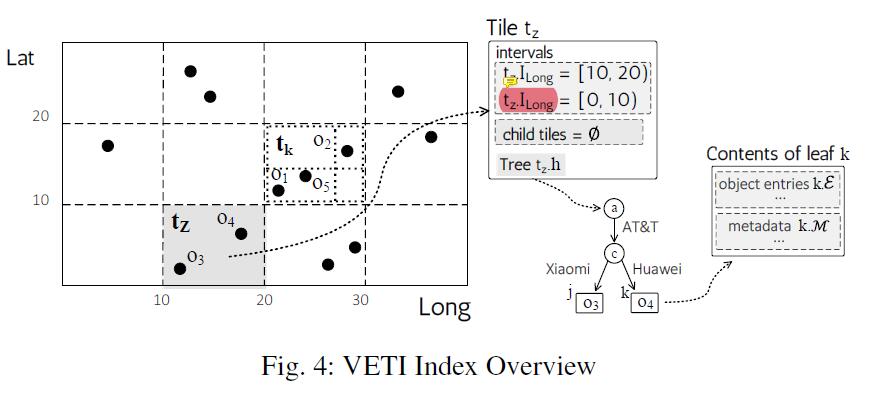
# VETI 初始化

VETI 初始化过程在第一次用户查询时构建。分如下步骤：

确定索引特征，即 $\mathbb{I}_\mathcal{T}$ 和对应 CET 结构的确定。
解析文件，填充索引
计算第一次用户查询

# 问题和方向

CMU 交互定理证明？
Cambridge also
type theory