首页

# 异质图

# 背景

在先前的研究中，研究的图中边的种类是唯一的。如果图中具有不同种类的节点和不同种类的边，那么该图称为一个异质图 (heterogeneous ghaphs).

我们主要讨论三种异质图：

  1. 关系图卷积神经网络 (Relational GCNs)
  2. 知识图谱 (Knowledge Graphs)
  3. 知识图谱补全 (Embeddings for KG Completion)

# 定义

一个异质图 (heterogeneous graph) 定义为一个四元组

G=(V,E,R,T)G = (V, E, R, T)

其中，

  • 具有不同类型的节点 vi∈Vv_i \in V;
  • 具有不同关系的边 (vi,r,vj)∈E(v_i, r, v_j) \in E;
  • 节点类型映射为 T(vi)T(v_i);
  • 关系类型 r∈Rr \in R.

由此可见，异质图的主要特征是具有不同类型的边。

# 例子

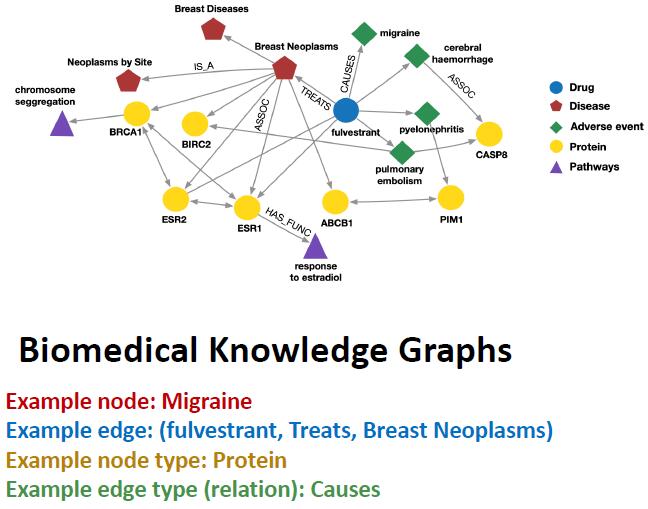
生物医学知识图谱 (Biomedical Knowledge Graphs) 是一个异质图。

生物医学知识图谱

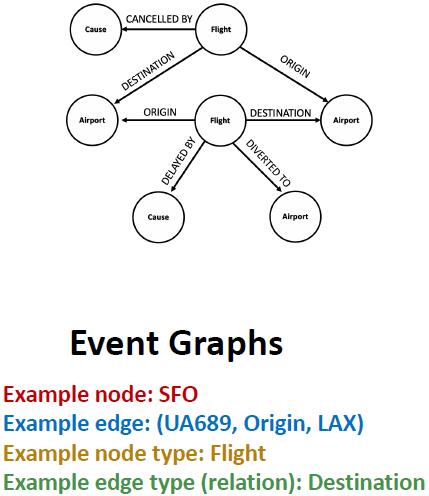
事件图 (Event Graphs) 也是一个异质图。

事件图

# 关系图卷积神经网络

# 基本 GNN 回顾

首先，让我们回顾基本的 GNN 架构。基于 MPNN 框架，GNN 的每一层可以分为下面两个过程：

  1. 消息传递：各节点计算获得的信息

    mu(l)=MSG(l)(ht(l−1)),u∈N(v)∪{v},\boldsymbol{m}_u^{(l)} = \mathrm{MSG}^{(l)}\left(\boldsymbol{h}_t^{(l-1)}\right), \quad u \in N(v) \cup \{v\},

  2. 聚合：聚合邻居信息

    hv(l)=AGG(l)({mu(l),u∈N(v)},mv(l)).\boldsymbol{h}_v^{(l)} = \mathrm{AGG}^{(l)}\left(\left\{\boldsymbol{m}_u^{(l)},\;u \in N(v)\right\}, \boldsymbol{m}_v^{(l)}\right).

GCN 的一层可以表示为

hv(l)=σ(W(l)∑u∈N(v)hu(l−1)∣N(v)∣).\boldsymbol{h}_v^{(l)} = \sigma\left(\boldsymbol{W}^{(l)} \sum_{u \in N(v)} \frac{\boldsymbol{h}_u^{(l-1)}}{|N(v)|}\right).

如果放到 MPNN 框架中，那么就将权重系数项放到求和内，即

hv(l)=σ(∑u∈N(v)W(l)hu(l−1)∣N(v)∣),\boldsymbol{h}_v^{(l)} = \sigma\left(\sum_{u \in N(v)} \boldsymbol{W}^{(l)} \frac{\boldsymbol{h}_u^{(l-1)}}{|N(v)|}\right),

其中

W(l)hu(l−1)∣N(v)∣\boldsymbol{W}^{(l)} \frac{\boldsymbol{h}_u^{(l-1)}}{|N(v)|}

项为消息计算，而求和为聚合过程。

那么很自然就能联想到，对于不同的边，赋予不同的权值就可以处理异质图了。

# 定义

我们将关系图卷积神经网络 (Relational GCN, RGCN) 的一层公式化表述为

\boldsymbol{h}_v^{(l+1)} = \sigma\left(\sum_{r \in R}\sum_{u \in N_v^r}\frac{1}{c_{v,r}}\boldsymbol{W}_r^{(l)}\boldsymbol{h}_{u}^{(l)} + \boldsymbol{W}_0\^{(l)}\boldsymbol{h}_v^{(l)} \right).

它显然也是位于 MPNN 框架下的，消息包括基于邻居节点的消息 mu,r(l)=1cv,rWr(l)hu(l)\boldsymbol{m}_{u,r}^{(l)} = \frac{1}{c_{v,r}} \boldsymbol{W}_r^{(l)}\boldsymbol{h}_{u}^{(l)} 和自环 \boldsymbol{m}_v^{(l)} = \boldsymbol{W}_0\^{(l)}\boldsymbol{h}_v^{(l)}, 聚合仍然是求和。

# 可扩展性

RGCN 的可扩展性 (Scalability) 可能是一个问题。对于每一类关系，需要层数 LL 个权重矩阵 Wr(1),Wr(2),…,Wr(L)\boldsymbol{W}_r^{(1)}, \boldsymbol{W}_r^{(2)}, \dots, \boldsymbol{W}_r^{(L)}. 其中，每个权重矩阵 Wr(l)\boldsymbol{W}_r^{(l)} 的大小 d(l+1)×d(l)d^{(l+1)} \times d^{(l)} 与嵌入维度有关。对于一般的问题，关系数目可能是 10310^3 或 10410^4 级别，嵌入维度是 10210^2 级别，且各矩阵可能是稠密的，因此参数过多，训练困难。下面，我们采用两种方式降低 RGCN 的参数数量。

# 利用块对角矩阵

将参数矩阵强行转化为块对角矩阵 (block diagonal matrices) 是一种降低参数的方法。这样存在的问题是，参数矩阵难以捕捉较远距离的两节点关系，但是可以通过多次消息传递解决。

假设将参数矩阵均分为 BB 个对角块，那么参数数量将从 d(l+1)×d(l)d^{(l+1)} \times d^{(l)} 降低到 B×(d(l+1)/B)×(d(l)/B)B \times (d^{(l+1)} /B)\times (d^{(l)}/B).

# 基学习

另一个降低参数的方式是实现多关系的权重共享，通俗地说就是将不同关系的权重矩阵分解为更基本的基，然后将权重矩阵表示为基矩阵的线性组合，因此得名基学习 (basis learning). 公式表述为

Wr=∑b=1BWrbar,bVb\boldsymbol{W}_r = \sum_{b=1}^B \boldsymbol{W}_r^b a_{r,b} \boldsymbol{V}_b

其中 Vb\boldsymbol{V}_b 是所有关系所共享的基矩阵，ar,ba_{r,b} 是基矩阵 Vb\boldsymbol{V}_b 对关系 rr 的权重。

这里依赖的一个基本假设是，不同关系是相关的。因此，相关程度的高低决定参数压缩的程度。假如所有的权重矩阵线性独立，那么该方法将无法实现参数压缩。

# 例子

RGCN 解决的任务包括两类：实体分类（节点分类）和链路预测。

对于实体分类问题，注意到 RGCN 的输出向量 hv(L)\boldsymbol{h}_v^{(L)} 可以表示节点特征，因此此类任务是显然可完成的。

对于链路预测问题，样本关系很有可能是不均衡的，因此在训练时需要进行预处理，使得每种类型的边出现在训练集的数目相同。关于最后的输出，需要权重矩阵一些 Wri\boldsymbol{W}_{r_i}. 对于节点 A,BA, B, 可以给出一个边属于关系 rir_i 的概率

fri(hA(L),hB(L))=hA(L)WrihB(L).f_{r_i}(\boldsymbol{h}_A^{(L)}, \boldsymbol{h}_B^{(L)}) = \boldsymbol{h}_A^{(L)}\boldsymbol{W}_{r_i}\boldsymbol{h}_B^{(L)}.

我很怀疑这样预处理的正确性... 抽空再看看原本的 paper. 但这部分与目前的研究不太相关，因此后续再说。

# 知识图谱与知识图谱补全

# 知识图谱

知识图谱 (Knowledge Graph, KG) 包括三个基本组成要素

  • 实体 (entities): 图上的节点
  • 类型 (types): 实体（节点）可以具有的类别
  • 关系 (relationships): 节点之间的边

知识图谱有两个基本特征：

  1. 庞大 (massive): 拥有 millions 级别的节点和连边；
  2. 不完全 (incomplete): 许多事实知识对应的边可能不出现在知识图谱中。

# 知识图谱的边表示

知识图谱中的边可以表示为一个三元组 (h,r,t)(h, r, t), 分别为

  • 头实体 (head entity): 边的起点
  • 关系 (relation): 边的类型
  • 尾实体 (tail entity): 边的终点

换句话说，箭头是从头指向尾的。所以箭头那边是尾节点。

对于不同的关系，头尾之间的紧密程度可能是不同的。衡量紧密程度可以通过嵌入的方式，一种经典的方法称为 TransE.

# TransE

我们希望边的三元组均找到嵌入，即对于 (h,r,t)(h,r,t), 分别定义其嵌入为 h,r,t∈Rd\boldsymbol{h}, \boldsymbol{r}, \boldsymbol{t} \in \mathbb{R}^d, 且当对应事实存在时，希望满足

h+r≈t,\boldsymbol{h} + \boldsymbol{r} \approx \boldsymbol{t},

否则希望

h+r≠t.\boldsymbol{h} + \boldsymbol{r} \neq \boldsymbol{t}.

这样，打分函数可以定义为

fr(h,t)=−∥h+r−t∥.f_r(h,t) = -\|\boldsymbol{h} + \boldsymbol{r} - \boldsymbol{t}\|.

算法的具体细节不再赘述，仍然是基于负采样和梯度下降的算法。

# 缺陷

# 知识图谱中的关系模式

在知识图谱中，可能蕴含有不同性质的关系模式。例如：

  • 对称性 (symmetry): 假如有边为 (h,"Roommate",t)(h, \text{"Roommate"}, t), 则边 (t,"Roommate",h)(t, \text{"Roommate"}, h) 也存在；
  • 逆关系 (inverse relation): 假如有边 (h,"Advisor",t)(h, \text{"Advisor"}, t), 则应该有 (t,"Advisee",h)(t, \text{"Advisee"}, h) 存在。

显然，TransE 并不能有效区分这两种不同的关系。

特殊的关系大概包括以下几类：

  • 对称 / 反对称 (symmetric/antisymmetric) 关系：

    r(h,t)⇒r(t,h)r(h,t)⇒¬r(t,h),∀h,t.r(h, t) \Rightarrow r(t, h) \quad r(h,t) \Rightarrow \neg r(t, h), \forall h, t.

  • 逆 (inverse) 关系：

    r2(h,t)⇒r1(t,h)r_2(h, t) \Rightarrow r_1(t, h)

  • 组合 / 传递 (Composition/Transitivity) 关系：

    r1(x,y)∧r2(y,z)⇒r3(x,z)∀x,y,zr_1(x,y) \wedge r_2(y,z) \Rightarrow r_3(x,z) \quad \forall x, y, z

  • 一对多 (1 to N) 关系：

    r(h,t1),r(h,t2),⋯,r(h,tn)are all true.r(h, t_1), r(h, t_2), \cdots, r(h, t_n) \text{ are all true.}

显然，TransE 不能建模上述关系中的对称关系和一对多关系，可以有效建模反对称、逆、传递关系。

# TransR

注意到，如果将上面提到的问题转化到一个更高维度的空间中，那么对称和一对多就可以表示了（这两者在本质上是统一的）。

TransR 就是采用此思想基于 TransE 的改进。通过乘一个高维矩阵，将其线性变换到另一个空间中作 TransE.