首页

# 图机器学习的传统方法 (Traditional Methods for ML on Graphs)

本节课程主要介绍了传统图机器学习中，图的各项特征是如何构建的。

# 回顾

传统的机器学习管线包括两个部分：

  • 设计关于节点 / 连边 / 图的特征
  • 训练机器学习模型并应用

在本课程中，我们将关注如何设计特征。

# 节点级别的任务和特征

# 节点级别任务

一个典型的节点级别的任务是一个半监督节点分类问题问题。大多数节点被染成了红色或绿色，部分节点为灰色。希望将灰色的节点染色。

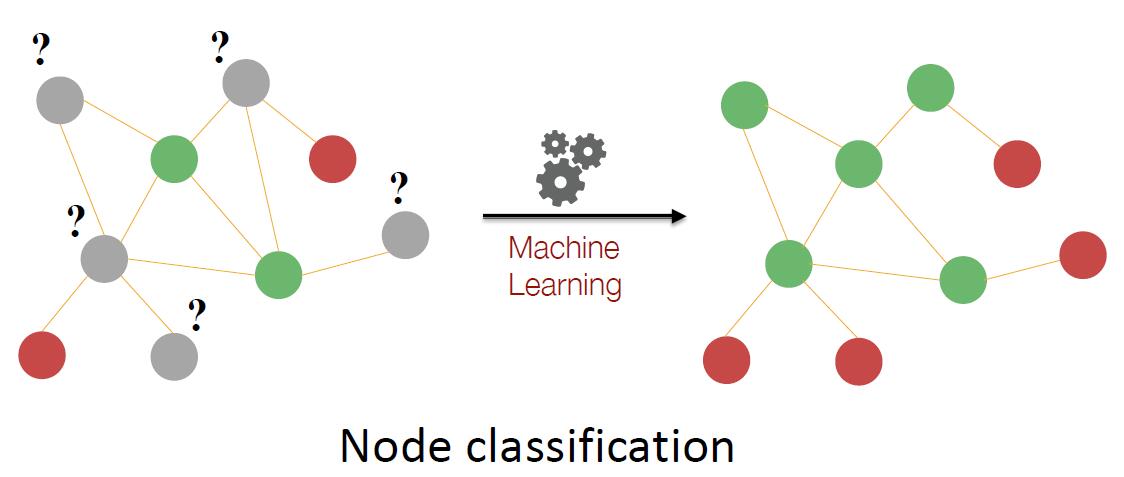
注意到，在该任务中，每个红色节点都是叶子节点，而绿色节点是非叶子节点。因此，我们的目标就是将节点在网络中的结构和位置进行特征化 (characterize the structure and position of a node in the network).

# 节点度

注意到，节点度是一种顶点特征，其特点是会将所有邻居视作等价的，没有区分邻居之间的重要关系。换句话说，如果仅将节点度信息作为特征，那么任何机器学习模型都不能区分不同的度相同的节点。

# 节点中心性

基于上述考虑，我们引入节点中心性 (node centrality) 的概念。顶点 vv 的顶点中心性 cvc_v 刻画了该顶点在一个图中的重要程度 (node importance in a graph).

刻画顶点中心性的方式有很多，包括

  • 度中心性 (degree centrality): 就是前述仅依靠节点度进行中心性刻画的方式。
  • 特征向量中心性 (engienvector centrality)
  • 介数中心性 (betweenness centrality)
  • 关联中心性 (closeness centrality)
  • others

# 特征向量中心性

一个简单的想法是，如果一个顶点 vv 被其余重要的顶点 u∈N(v)u \in N(v) 包围，那么该顶点是重要的。于是可以定义特征向量中心性 (eigenvector centrality) 如下

cv=1λ∑u∈N(v)cuc_v = \frac{1}{\lambda}\sum_{u \in N(v)} c_u

结合邻接矩阵的定义，我们可以将其转化为

λc=Ac\lambda \boldsymbol{c} = A\boldsymbol{c}

其中 λ\lambda 是一个确定的正值， AA 是邻接矩阵，c\boldsymbol{c} 是中心性向量 (centrality vector).

c\boldsymbol{c} 的含义是什么？基于 cv=1λ∑u∈N(v)cuc_v = \frac{1}{\lambda}\sum_{u \in N(v)} c_u 定义，可以得到 c={cu}\boldsymbol{c} = \{c_u\} 就是各节点中心性组成的向量。

仔细想想，便发现上述转化还是很有趣的。其将邻居节点的相互依赖问题转化为了特征向量的求值问题，使得可以直接解出各个顶点的特征。

基于 Perron-Frobenius 定理，图中的最大特征值 λmax⁡\lambda_{\max} 是正值，且是唯一的 (无重根)，对应的特征向量 cmax⁡\boldsymbol{c}_{\max} 用作图中心性的评价。

# 介数中心性

介数中心性 (betweenness centrality) 是基于图最短路的一种中心性度量。其源于这样一个想法：如果一个顶点 vv 位于越多的最短路径中，那么该顶点是越重要的。基于此，介数中心性定义为

cv=∑s≠v≠tσst(v)σstc_v = \sum_{s \neq v \neq t} \frac{\sigma_{st}(v)}{\sigma_{st}}

其中 σst\sigma_{st} 表示从顶点 ss 到 tt 的最短路径数目，σst(v)\sigma_{st}(v) 表示经过顶点 vv 的最短路径数目。

例如，在下图中，节点 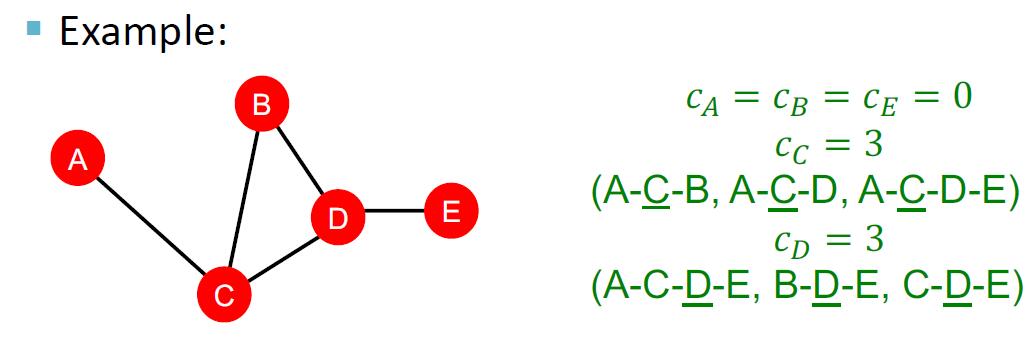C,DC, D 的中心度为 33.

显然，介数中心性的最小取值为 00, 而最大取值为 (N−1)(N−2)/2(N-1)(N-2)/2, 其中 NN 为节点数。因此，有两种常见的归一化方法：

  1. 将介数中心性同除 (N−1)(N−2)/2(N-1)(N-2)/2. （有向图为 (N−1)(N−2)(N-1)(N-2)）
  2. 采用 normal(g(n))=g(v)−min⁡(g)max⁡(g)−min⁡(g)\displaystyle \mathrm{normal}(g(n)) = \frac{g(v) - \min(g)}{\max(g) - \min(g)}.

# 关联中心性

关联中心性 (closeness centrality) 同样是基于图最短路的一种中心性度量。其想法是：如果一个顶点到图中其它顶点的距离最短，那么该顶点就最重要。其定义为

cv=1∑u≠vd(u,v)c_v = \frac{1}{\sum_{u \neq v} d(u,v)}

其中 d(u,v)d(u,v) 表示从顶点 uu 到 vv 的最短路径长度。下面是一个关联中心性的例子：

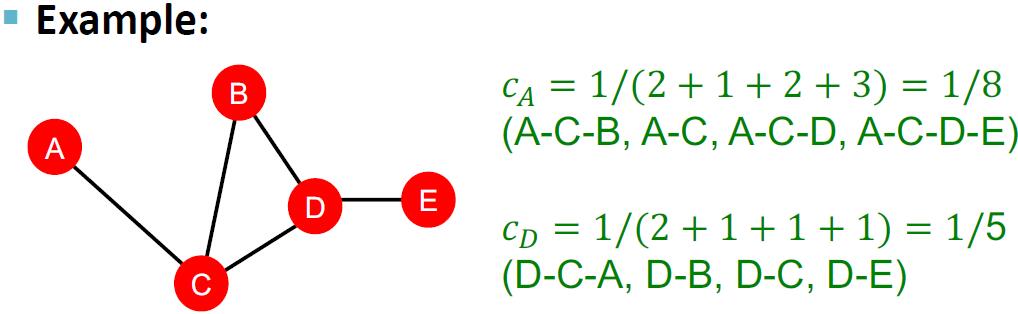
显然，这样的定义使得关联中心性的值最大为 1N−1\frac{1}{N-1}, 因此可以对其进行归一化：

cv=N−1∑u≠vd(u,v)c_v = \frac{N-1}{\sum_{u \neq v} d(u,v)}

在许多网络中，已经证明归一化的关联中心性与对应点的度对数有近似线性关系，即

1cv=−ln⁡(kv)ln⁡(z−1)+β\frac{1}{c_v} = - \frac{\ln (k_v)}{\ln (z-1)} + \beta

其中 kvk_v 是节点 vv 的度，zz 被称作分支因子 (branching factor), 代表计算该节点的关联中心性时最短路径树的平均度（不包括根和叶子节点）。β\beta 是一个参数。

# 聚类系数

现在，我们来考虑节点所在的局部结构。基于此的一种经典度量为聚类系数 (clustering coefficient), 用来衡量节点邻居间的联系程度。其定义为：

ev=∣{est∈E∣s,t∈N(v)}∣(kv2)∈[0,1]e_v = \frac{|\{e_{st} \in E|s,t \in N(v)\}|}{\binom{k_v}{2}} \in [0, 1]

其中 kvk_v 是节点 vv 的度。

可以观察到，聚类系数实际上是衡量顶点所在的自我网络 (ego-network) 中的三角形个数。

# Graphlets & GDV

基于上述三角形的观察，我们希望抽象出一种基于三角形的子结构。在这里，我们定义小图 (graphlet) 为有根连通非同构子图 (rooted connected non-isomorphic graphs).

graphlet 似乎还没有一个广泛使用的中文翻译，但是翻译成小图似乎勉强可以，毕竟 wavelet 可以翻译成小波。在下面的笔记中，尽量采用 graphlet 词本身。

更多的内容，可以参考 Wikipedia: Graphlets.

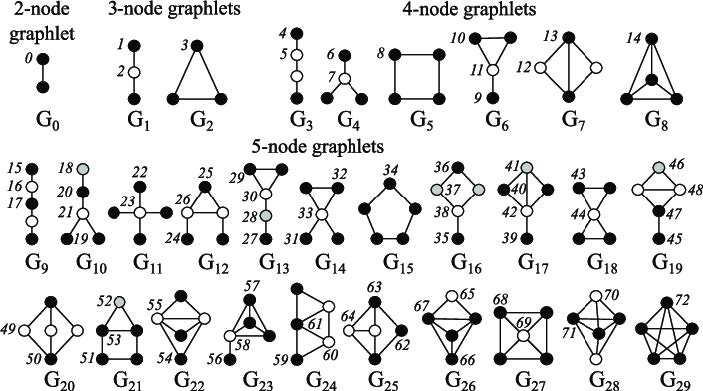
注意到，在上图中，对于三节点 graphlets, 其共有 33 种，因为对于 G1G_1, 其存在两种不同的节点。（图中的顶点颜色是为了区分地位不等价的节点）

梦回高考化学同分异构体计数

基于上述的 graphlets, 我们可以定义 小图度向量 (graphlet degree vector, GDV). 它的每一维度实际上是表示以该节点为根，对应的 graphlet 的数量。例如，如果仅研究上图标号中的 G0G_0, 那么节点的 GDV 实际上是节点度。下面是一个仅研究两节点和三节点的 graphlet 的 GDV 的例子：

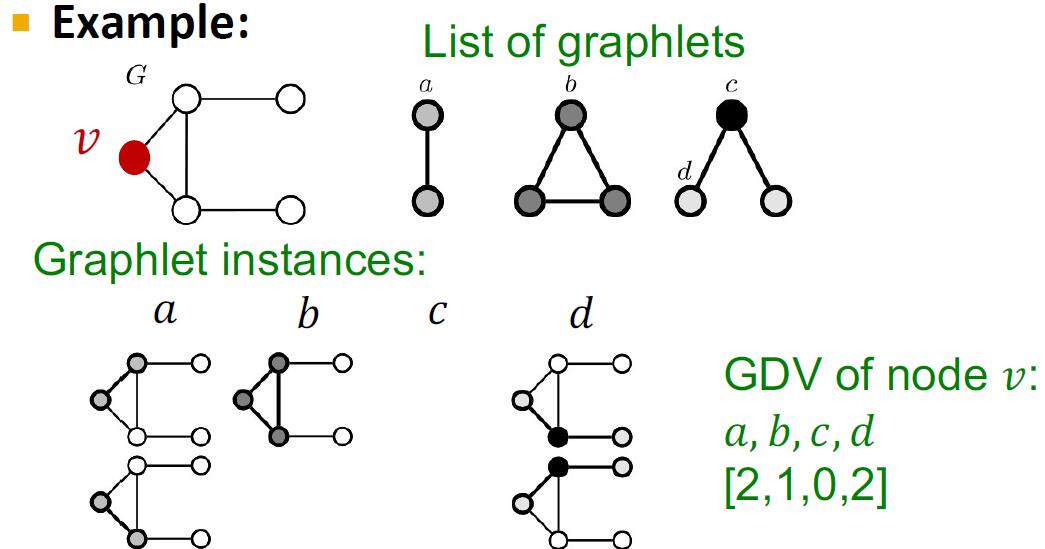
如果我们研究至多五个节点的 graphlets, 那么就可以得到 7373 个维度的 GDV. 所以，GDV 实际上是采用更加细致的结构 (不同的 graphlets) 进行节点局部拓扑结构的表示，或者说 embedding.

# 总结

节点特征实际上可以归纳为两类：

  • 基于重要性的特征 (importance-based features)
    • 节点度
    • 不同类型的节点中心性
  • 基于结构的特征 (structure-based features)
    • 节点度
    • 聚类系数
    • GDV

# 边级别任务和特征

# 边级别任务

一个边级别的典型任务是基于图中已有的边预测新的边。这实际上是将图中所有未存在链接的节点对进行可能性排序，选取 top KK 作为预测的结果。进一步地，其一般包括两种范式：

  • 边的随机丢失问题 (links missing at random): 图中的边按照某概率随机丢失，希望预测丢失的边集合。
  • 时序的边预测问题 (links over time): 时序上边是逐渐增加的，希望基于过去信息预测未来边的增加情况。例如引文网络等社交网络。

注意到，如果仅采用前面提到的节点特征进行训练，那么会缺失许多节点间关系的信息。

因此，我们需要做的就是对于图中的所有节点对 (x,y)(x,y), 预测一个分数 c(x,y)c(x,y), 然后将节点对按分数高低排序，最后给出预测。

# 边级别特征概述

一般有三类常见的边特征化方法：

  • 基于距离的特征 (distance-based features)
  • 局部邻域重叠特征 (local neighborhood overlap features)
  • 全局邻域重叠特征 (global neighborhood overlap features)

# 基于距离的特征

一种最简单的想法是考虑两点之间的最短路长度。下图是一个例子。

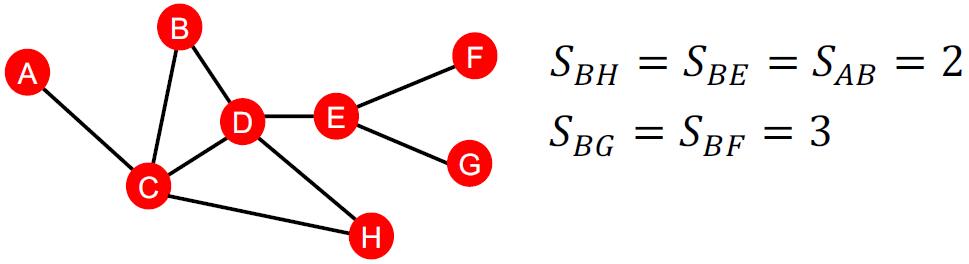
注意到，基于最短路的特征不能捕获邻域间重叠的程度，也不能捕获节点间连接的强度。

# 局部邻域重叠特征

对于两节点 v1,v2v_1, v_2, 基于局部邻域重叠的特征包括以下几种：

  1. 共同邻居数 (common neighbors): ∣N(v1)∩N(v2)∣|N(v_1) \cap N(v_2)|.
  2. Jaccard 系数 (Jaccard's coefficient): ∣N(v1)∩N(v2)∣∣N(v1)∪N(v2)∣\displaystyle \frac{|N(v_1) \cap N(v_2)|}{|N(v_1) \cup N(v_2)|}. 这样定义是希望通过规范化，降低高度节点带来的影响。
  3. Adamic-Adar 指数 (Adamic-Adar index): ∑u∈N(v1)∩N(v2)1log(∣N(u)∣)\displaystyle \sum_{u \in N(v_1) \cap N(v_2)} \frac{1}{log(|N(u)|)}. 这样实际上是尝试减少共同邻居中的高度节点带来的影响。在社交网络中，这种做法有显著效果。
  4. Preferential Attachment 指数 (Preferential Attachment index): ∑u∈N(v1)∩N(v2)1∣N(u)∣\displaystyle \sum_{u \in N(v_1) \cap N(v_2)} \frac{1}{|N(u)|}. （额... 这是代码补全自动给我补充上的，课程中没有）

需要注意的是，局部邻域重叠特征具有一定的局限性。如果两节点之间没有共同邻居，那么不论采用何种计算方式，其局部邻域重叠特征的值都是 00. 然而，两节点仍然可能在未来相连。因此，我们需要引入全局的重叠邻域特征，来避免这种错误。

# 全局重叠邻域特征

# Katz 指数

Katz 指数 (Katx index) 计算两节点 v1v_1, v2v_2 之间的所有路径，且对不同长度的路径赋予一个不同的衰减指数。

Sv1v2=∑l=1∞βlAv1v2lS_{v_1v_2} = \sum_{l=1}^\infty \beta^l A_{v_1v_2}^l

其中，AA 是图的邻接矩阵，β\beta 是一个衰减系数 (discount factor), 表明越长的路径其重要性越低。

注意到，这实际上是一个等比求和，因此我们可以得到该表达的闭式解 (close form) 如下：

S=∑i=1∞βiAi=(I−βA)−1−IS = \sum_{i=1}^\infty \beta^i A^i = (I - \beta A)^{-1} -I

邻接矩阵的幂 AkA^k 可以用来表示图中长度为 kk 的路径数目。

# 图级别特征和图核

# 概述

设计图基本特征的目标是特征化整个图的结构。在这里，我们需要采用核方法。

核方法简介

核方法 (kernel methods) 的核心是绕开特征向量直接计算相似度。

一些其它小知识：

  1. 核函数 K(G,G′)∈RK(G, G') \in \mathbb{R} 的作用是基于数据度量相似性。
  2. 核矩阵 K=(K(G,G′))G,G′\boldsymbol{K} = (K(G, G'))_{G, G'} 是半正定矩阵，具有非负特征值。
  3. 存在一种特征表示 ϕ(⋅)\phi(\cdot) 使得 K(G,G′)=ϕ(G)⊤ϕ(G′)K(G, G') = \phi(G)^\top \phi(G'). 但 ϕ(G)\phi(G) 通常不需要显式计算，这就是核方法的优势。
  4. 一旦定义了核函数，我们就可以采用 SVM 进行高效预测。

# 关键思想

设计图核的目标是设计图特征向量 ϕ(G)\phi(G). 其关键思想是使用词袋 (bag-of-words, BoW) 进行设计。

词袋是自然语言处理领域的方法，它可以将文本表示为词频向量，其核心是忽略词语之间的顺序关系。

例如，基于 BoW 思想，我们可以设计度核，让特征向量的第 kk 个维度表示图中度为 kk 的节点数目，如下图所示：

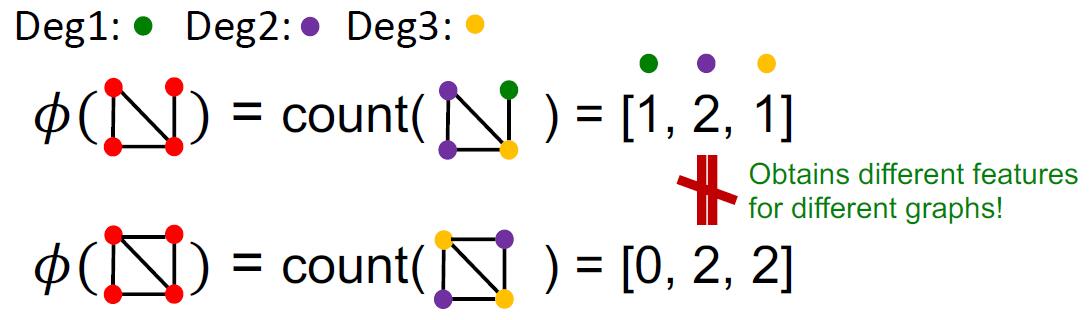
下面将介绍的两种图方法也是基于 BoW 思想设计的，但是它们采用的特征更加复杂。

# 小图核

# 小图特征的想法与例子

小图特征 (graphlet feature) 的想法是对图中的不同 graphlets 进行计数。但与节点级特征中 graphlet 方法不同的是，此处的 graphlets 是无根的，且此处的 graphlet 不一定是连通图。

下面是一个例子：

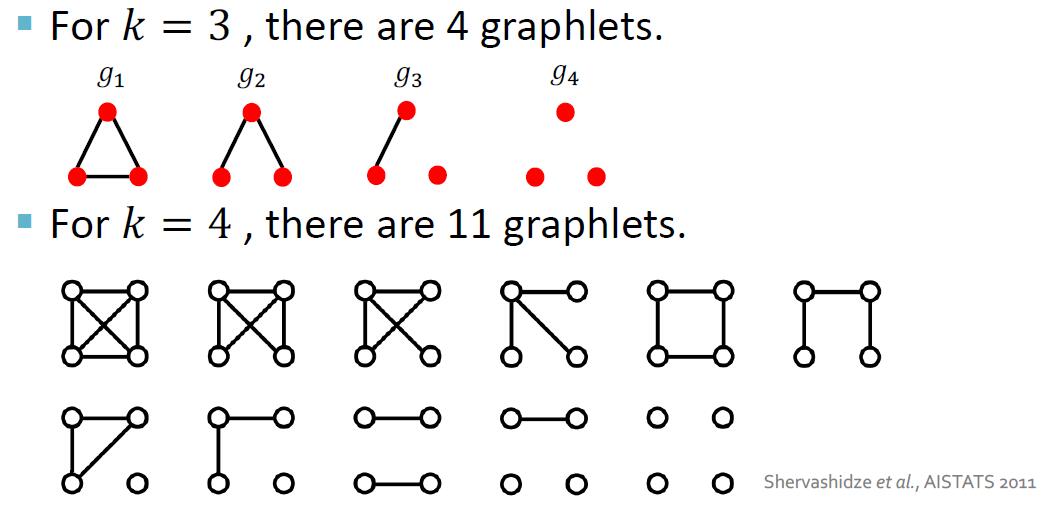
这样，对于一个图 GG, 我们可以给出一个小图表 Gk=(g1,g2,…,gnk)\mathcal{G}_k = (g_1, g_2, \dots, g_{n_k}), 并定义小图计数向量 (graphlet count vector) fG∈Rnk\boldsymbol{f}_G \in \mathbb{R}^{n_k} 如下：

(fG)i=∣{gi⊆G}∣,i=1,2,…,nk.(\boldsymbol{f}_G)_i = |\{g_i \subseteq G\}|, i = 1, 2, \dots, n_k.

# 小图核的定义

对于图 G,G′G, G', 我们定义 graphlet 核 K(G,G′)=fG⊤fG′K(G, G') = \boldsymbol{f}_G^\top\boldsymbol{f}_{G'}.

# 小图核的局限和变种

当计算 K(G,G′)K(G, G') 时，如果 GG 与 G′G' 在尺度上差异巨大，那么 graphlets 的计数值也会相差巨大，因此可能会导致某些维度的信息被忽略。于是，可以将特征向量进行归一化来解决此问题。归一化的向量可以表示为

hG=fGSum(fG),\boldsymbol{h}_G = \frac{\boldsymbol{f}_G}{\mathrm{Sum}(\boldsymbol{f}_G)},

其中，Sum(fG)\mathrm{Sum}(\boldsymbol{f}_G) 表示对特征向量中的每个元素进行求和。于是可以定义归一化 graphlet 核为

K(G,G′)=hG⊤hG′.K(G, G') = \boldsymbol{h}_G^\top\boldsymbol{h}_{G'}.

采用 graphlet 核的一个重要问题是，计算 graphlet 核的时间复杂度为 O(∣V∣2ℓ)O(|V|^{2\ell}), 其中 ℓ\ell 表示 graphlet 的长度。因此该方法是极其昂贵的。

此外，计算两个图是否同构是 NP-hard 的，因此对于尺度较大的 graphlets, 计算 graphlet 核的复杂度将变得很高。

# Weisfeiler-Lehman 核

# 算法

Weisfeiler-Lehman 核 (Weisfeiler-Lehman kernel) 的想法是借助邻域结构迭代地扩充节点的表达。实现这一目标的算法称为 Weisfeiler-Lehman 图同构检验 (Weisfeiler-Lehman graph isomorphism test), 又称 color refinement.

Weisfeiler-Lehman 图同构检验的迭代算法可以得到一个图的特征，其输入为一个图 GG. 算法流程如下：

  1. 我们对图中所有节点赋相同初始值（相同颜色）
  2. 按如下公式进行迭代：

    c(k+1)(v)=HASH({c(k)(v),{c(k)(u)}u∈N(v)}),c^{(k+1)}(v) = \mathrm{HASH}\left(\left\{c^{(k)}(v), \left\{c^{(k)}(u)\right\}_{u \in N(v)}\right\}\right),

    其中 HASH\mathrm{HASH} 是一个颜色映射函数，将颜色集合映射为一个新的颜色，要求不存在哈希冲突。
  3. 在 KK 步迭代后，c(k)(v)c^{(k)}(v) 就是一个集合了 KK 跳邻居的表示。

这不就是 Message Passing 嘛！但是这个想法是 2011 年的 paper. 或许这表示了人类手工设计特征的极限。

# 例子

下面是一个例子：




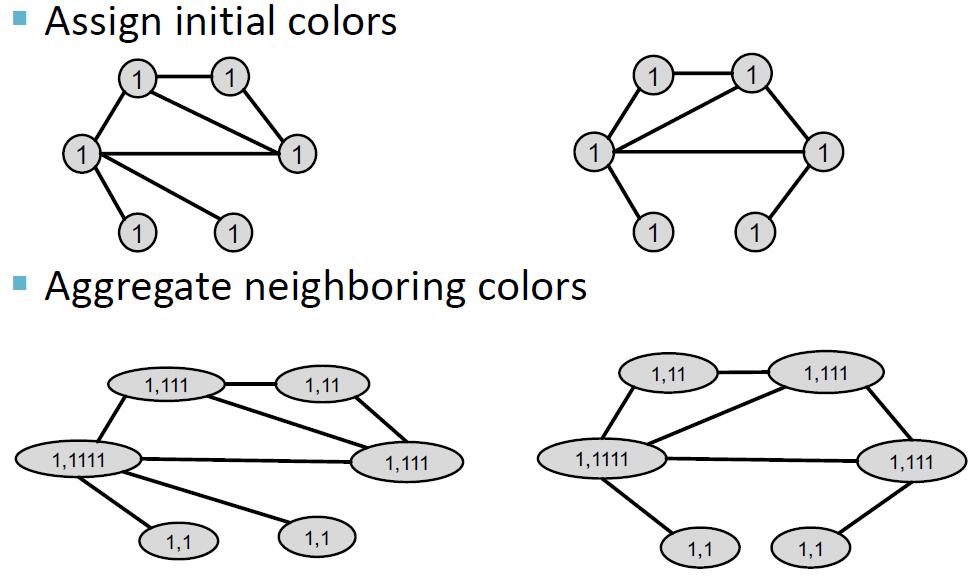
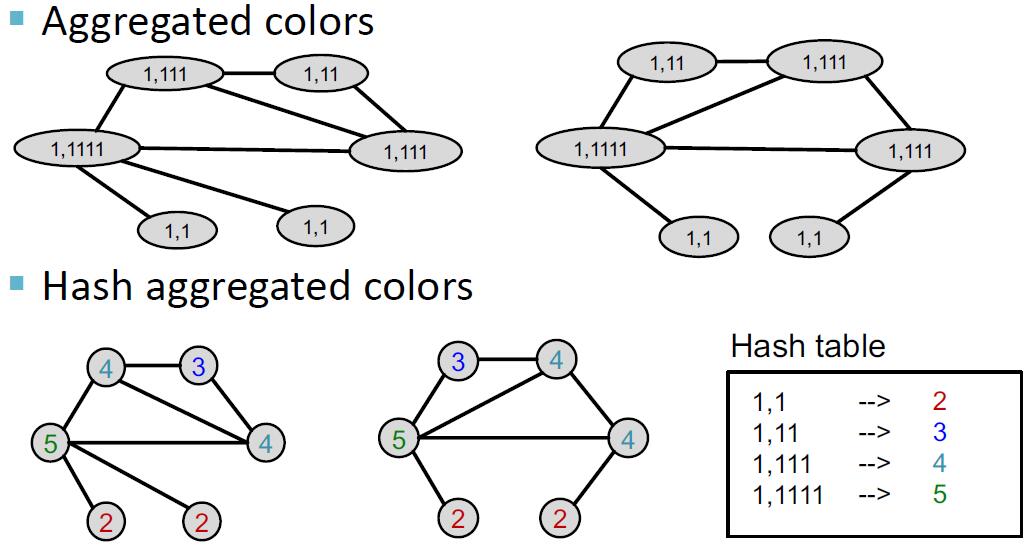
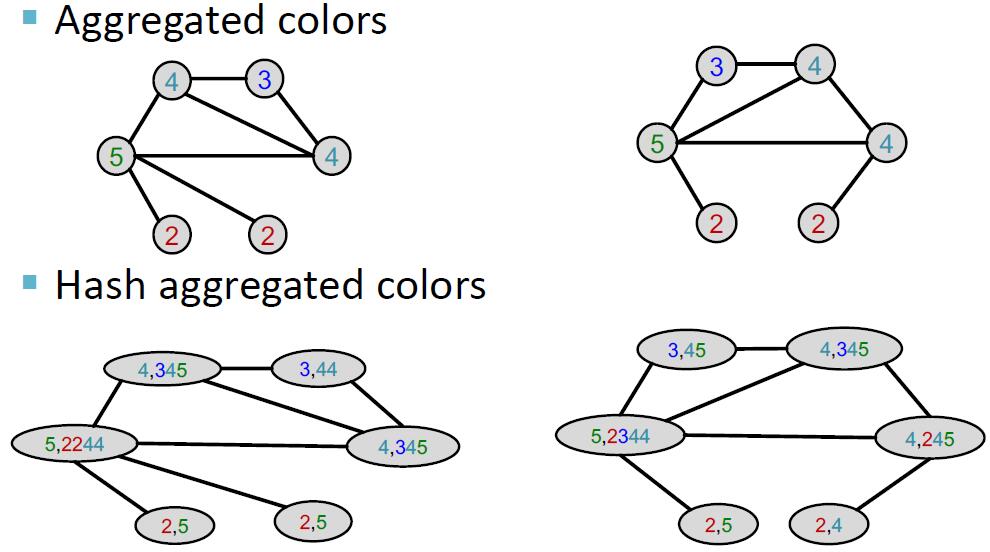
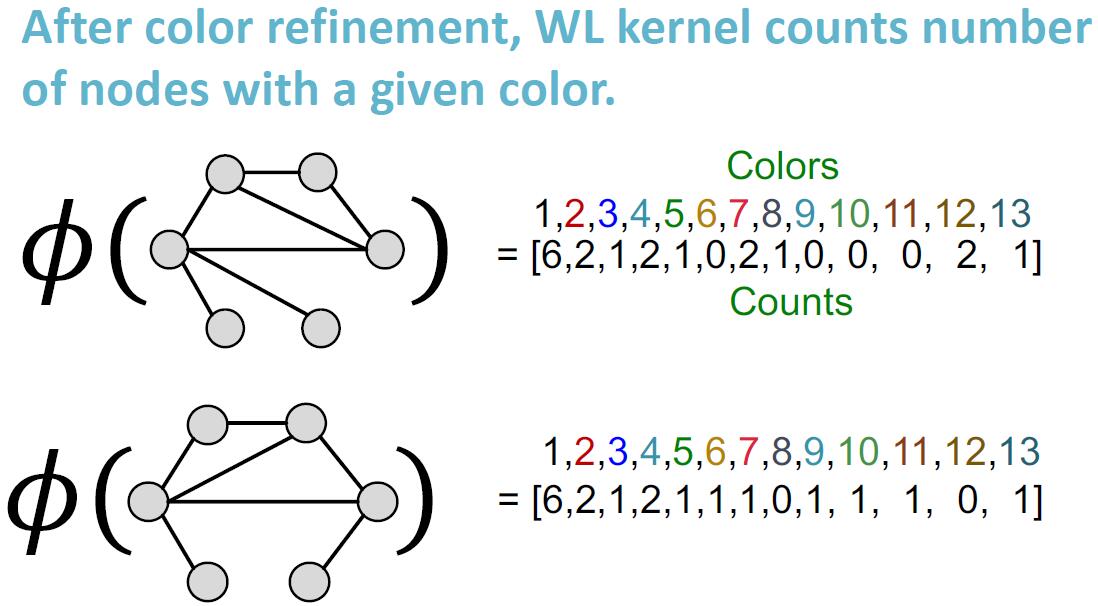
# 复杂度

Weisfeiler-Lehman 图同构检验的复杂度为 O(∣E∣×K)O(|E| \times K), 其中 KK 是迭代次数。注意到，迭代次数最高为 ∣V∣|V|, 因此该算法是高效的。