# 传统图机器学习方法回顾

在上一节中，我们梳理了传统图机器学习方法的主要知识。传统的图机器学习流程如下：

1. 输入图
2. 特征构建
3. 学习算法
4. 预测

其中，绝大多数精力被耗费在特征工程上（即第二步）。因此，一个自然的问题是，能否将特征提取自动化？这就是图表示学习 (graph representation learning). 我们将一个对象转化成的特征向量称为一个特征表示 (feature representation), 也称为一个嵌入 (embedding).

# 嵌入

设计嵌入方法时，我们需要保证相似度的近似不变。即嵌入前的对象如果相似，那么嵌入后的向量也应该尽量相似。

我们应该完成的内容如下：

1. 一个编码器 (encoder) $\mathrm{ENC}(\cdot)$: 将节点映射到嵌入
2. 一个节点相似度函数 (node similarity function) $\mathrm{similarity}(\cdot, \cdot)$: 用来计算原有网络中的节点相似度
3. 一个解码器 (decoder) $\mathrm{DEC}(\cdot)$: 将嵌入映射到相似分数 (similarity score), 一般选用点积即可。
4. 对编码器进行参数优化，使得 $\mathrm{similarity}(u,v) \approx \boldsymbol{z}_v^\top \boldsymbol{z}_u$.

# 编码器

一种最简单的编码器设计（称为 “浅层” 编码器 (shallow encoder)）是一个嵌入查找 (embedding-lookup) 矩阵。这样，就有

$$\mathrm{ENC}(v) = \boldsymbol{z}_v = Z\boldsymbol{v}$$

其中，$Z \in \mathbb{R}^{d \times |V|}$ 是我们需要优化的对象，而 $\boldsymbol{v} = \mathbb{I}^{|V|}$ 是一个示性向量 (indicator vector), 即采用 one-hot 编码。因此，$Z$ 的每一列存储了一个节点 $v$ 的嵌入。这样，对于规模特别大的图，该编码器参数众多，难以训练。因为对该编码器训练的实质是对各个节点分别训练。

# 节点相似度

在 encoder-decoder 框架下，一个重要问题就是节点相似度的定义问题。实际上，不同的节点相似度定义是图表示学习中不同方法区分的关键。

# 基于随机游走的节点嵌入算法

# 记号

在这里，我们需要预先定义一些常用的函数和记号：

• 向量 $\boldsymbol{z}_u$: 节点 $u$ 的嵌入。
• 概率 $P(v|\boldsymbol{z}_u)$: 从节点 $u$ 出发，经随机游走到达 $v$ 的（预测）概率。
• softmax 函数 $\sigma(\cdot)$: 将 $K$ 维向量归一化，$\sigma(z)_i = \frac{\exp(\boldsymbol{z}_i)}{\sum_{j=1}^K \exp(\boldsymbol{z}_j)}$.
• sigmoid 函数 $S(x) = \frac{1}{1+\exp(-x)}$: S - 型函数，将实数值转化为 $(0,1)$ 区间值。

# 基于随机游走的节点嵌入概述

# 随机游走

随机游走 (random walk) 是一种在图上进行游走的过程。输入一个图和图上的一个起始节点，然后随机移动到该节点的一个邻居节点，依次迭代下去。

这样，我们可以用一个随机游走过程中 $u, v$ 两点共同出现的概率来表示节点 $u$ 和 $v$ 的相似度。于是，对于某随机游走采样策略 $R$, 从节点 $u$ 出发到达节点 $v$ 的概率 $P_R(v|u)$ 是可计算的。随后，我们希望进行优化，使得嵌入可以正确编码随机游走带来的相似度，即 $\theta \propto P_R(v|u)$, 其中 $\theta$ 余弦相似度对应的夹角。

# 为什么采用随机游走？

为什么采用随机游走表示相似度？

1. 表现力强 (expressive): 如果一个节点可以通过随机游走高概率抵达另一个节点，那么说明两节点关系紧密，相似度强。此外，随机游走可以很好整合邻居信息。
2. 高效 (effective): 在计算相似度时不需要考虑所有节点，只需要考虑共同出现的随机游走过程。

# 随机游走嵌入转化为优化问题

那么，如何将上述随机游走相似度的定义放入到优化问题中？

输入一个图 $G = (V, E)$. 我们的目标是学习一个映射 $f:u \to \mathbb{R}^d$, $f(u) = \boldsymbol{z}_u$. 于是采用极大似然估计：

$$\max \sum_{u \in V} \log P\left(N_R(u)|\boldsymbol{z}_u\right),$$

其中，$N_R(u)$ 代表在某邻居选择策略 $R$ 下，节点 $u$ 的邻居。

# 算法框架

基于上述分析，一个通用的，基于随机游走的节点嵌入算法框架如下：

1. 基于某邻居选择策略 $R$, 从图上各个点 $u$ 开始，运行固定长度 $l$ 的随机游走。
2. 对每个节点 $u$, 构建基于上述策略 $R$ 的邻居多重集 $N_R(u)$.
3. 对嵌入进行最优化，依据的评判标准是给定节点 $u$ 的邻居多重集 $N_R(u)$, 最大化 $\sum_{u \in V} \log P\left(N_R(u)|\boldsymbol{z}_u\right)$.

# 邻居相似度衡量

在上述算法框架中，一个未解决的问题是，如何计算

$$\max \sum_{u \in V} \log P\left(N_R(u)|\boldsymbol{z}_u\right).$$

这等价于最小化损失函数

$$\mathcal{L} = \sum_{u \in V}\sum_{v \in N_R(u)} -\log (P(v|\boldsymbol{z}_u)).$$

然而，此处的概率 $P$ 仍未定义。采用 softmax 函数进行定义：

$$P(v|\boldsymbol{z}_u) = \frac{\exp(\boldsymbol{z}_u^\top \boldsymbol{z}_v)}{\sum_{n \in V}\exp (\boldsymbol{z}_u^\top \boldsymbol{z}_n)}$$

于是，我们将问题转化为对于不同的嵌入 $\boldsymbol{z}$, 求

$$\mathcal{L} = \sum_{u \in V}\sum_{v \in N_R(u)} -\log \left(\frac{\exp(\boldsymbol{z}_u^\top \boldsymbol{z}_v)}{\sum_{n \in V}\boldsymbol{z}_u^\top \boldsymbol{z}_n}\right)$$

的最小值。

# DeepWalk 算法

注意到，如果选取最简单的策略 $R$, 即使得 $N_R(u)$ 就是图中节点 $u$ 之外的所有节点，那么上述损失函数的计算复杂度是 $\mathcal{O}(|V|^2)$ 的。这是极其昂贵的。

DeepWalk 算法的想法是降低 softmax 函数中分母的计算范围。其仿照 Distributed representations of sentences and documents, 采用负采样方法 $R$ 进行概率估计，进而大幅降低计算复杂度。

# 负采样

那就先来介绍一下负采样方法。

负采样 (negative sampling) 方法

公式表述如下：

$$\log\left(\frac{\exp(\boldsymbol{z}_u^\top\boldsymbol{z}_v)}{\sum_{n \in V}\boldsymbol{z}_u^\top\boldsymbol{z}_n}\right) \approx \log (\sigma(\boldsymbol{z}_u^\top\boldsymbol{z}_v)) - \sum_{i=1}^k \log(\sigma(\boldsymbol{z}_u^\top\boldsymbol{z}_{n_i}), \quad n_i \sim P_V$$

即使是对于规模达到 $10^6$ 规模的节点，采样取 $k \in [5, 20]$ 也基本可以满足要求。

# 总结

1. 从图上每个节点开始进行固定长度的随机游走
2. 对于每一个节点 $u$, 收集随机游走过程中访问的节点，作为的邻居节点多重集 $N_R(u)$;
3. 采用随机梯度下降算法进行嵌入最优化：

   $$\mathcal{L} = \sum_{u \in V}\sum_{v \in N_R(u)} -\log (P(v|\boldsymbol{z}_u)).$$

# node2vec

相比于前面提到的 DeepWalk 算法，node2vec 希望 Random Walk 的游走策略选择中具有更大的灵活度和更强的归纳偏置 (bias), 这实际上是在全局和局部特征中进行权衡。 BFS 倾向于探索局部特征，而 DFS 倾向于探索全局特征。因此，我们可以在 BFS 和 DFS 之间进行权衡，以更好地捕获节点之间的依赖关系。

在 node2vec 中，我们引入两个参数 $p$ 和 $q$:

• $p$ 为返回参数 (return parameter), 表示回到上一状态的概率
• $q$ 为扩展参数 (in-out parameter), 表示此次探索采用 BFS 还是 DFS 的概率.

这种随机游走策略被称为二阶随机游走 (second-order random walk).

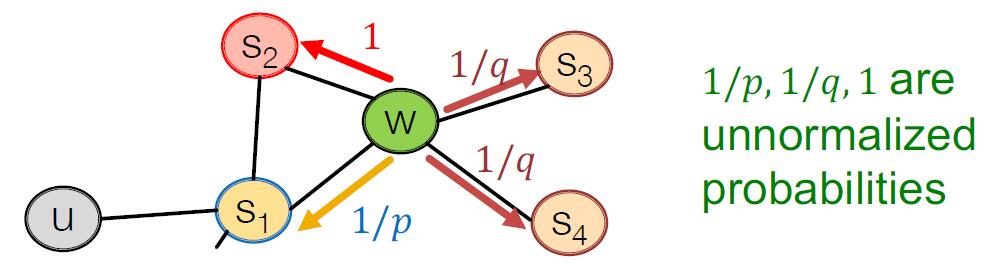
# 算法流程

因此，算法流程如下：

1. 计算随机游走各策略概率
2. 进行 $r$ 次长度为 $l$, 起点为 $u$ 的随机游走模拟
3. 采用 SGD 进行目标优化

# 图嵌入

现在，我们的目标是将一个子图或整个图 $G$, 做嵌入，得到图嵌入 $\boldsymbol{z}_G$.

在这里，一个基本的想法是对图中的所有节点嵌入表示求和，即

$$\boldsymbol{z}_G = \sum_{v \in V} \boldsymbol{z}_v.$$

该想法在 2016 年的 Convolutional Networks on Graphs for Learning Molecular Fingerprints 中被用来进行分子分类，取得了不错的效果。

第二个基本的想法是引入一个虚拟节点表示这个图，然后在该虚拟节点上运行节点嵌入。

该想法在 2016 年的 Gated Graph Sequence Neural Networks 中被提出。

# 匿名游走嵌入

第三个想法称为匿名游走嵌入 (Anonymous Walk Embedding, AWE). 提出于 ICML 2018 的文章 Anonymous Walk Embeddings. 该想法同样是基于随机游走思想探测图结构，但是放弃了图中具体顶点的信息。而是将游走路径中新增的节点依次赋予索引，按照索引分布进行图的嵌入表示。例如，在下图中的 A->B->C->B->C 和 C->D->B->D->B 都抽象为同一路径。

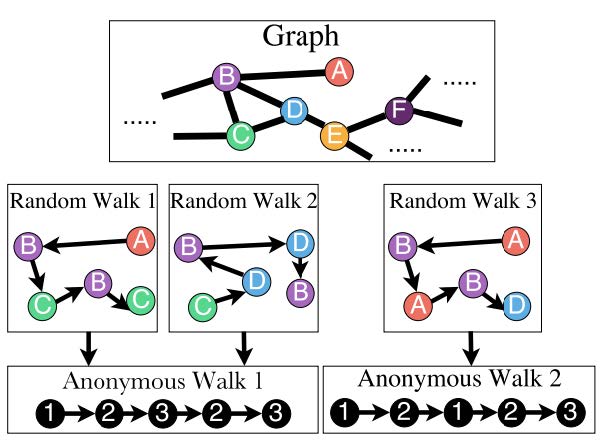
这样，我们可以仿照 Graphlet Kernel 的想法，按照路径的长度进行图子结构的计数。这样，对于长度为 $l$ 的路径，我们就可以得到一个长度为 $B_l$ 的向量，其中的每个维度代表图中该匿名路径的频数。

于是，引入的问题是：多少次匿名路径采样 $m$ 就足够了？

我们采用 $\varepsilon-\delta$ 语言描述。若将图 $G$ 的真实匿名路径分布记作 $\mathfrak{D}$, 利用长度为 $l$ 的匿名路径采样 $m$ 次得到的经验分布记作 $\mathfrak{D}^m$, 那么使得 $P\{\|\mathfrak{D}^m-\mathfrak{D}\|_1 \geq \varepsilon\} \leq \delta$ 的 $m$ 满足：

$$m = \left\lceil\frac{2}{\varepsilon^2}(\log(2^{B_l}-2) - \log \delta)\right\rceil.$$

# data-driven AWE

相比于直接按照频率进行嵌入，我们还可以从匿名随机游走中学习嵌入。这一想法同样来自于 Approach 3 对应的文章 Anonymous Walk Embeddings 和 word2vec (Distributed representations of sentences and documents).

如果将文章的想法直接类比到 word2vec, 那么每一个匿名游走是一个单词，一系列被同时采样的匿名游走构成一个词袋集合 (a set of co-occurring words), 一个图就是一个文档。这是类似于 DeepWalk

# 层次嵌入

图常常带有显著的社群特征，因此可以考虑进行层次嵌入 (hierarchical embedding).

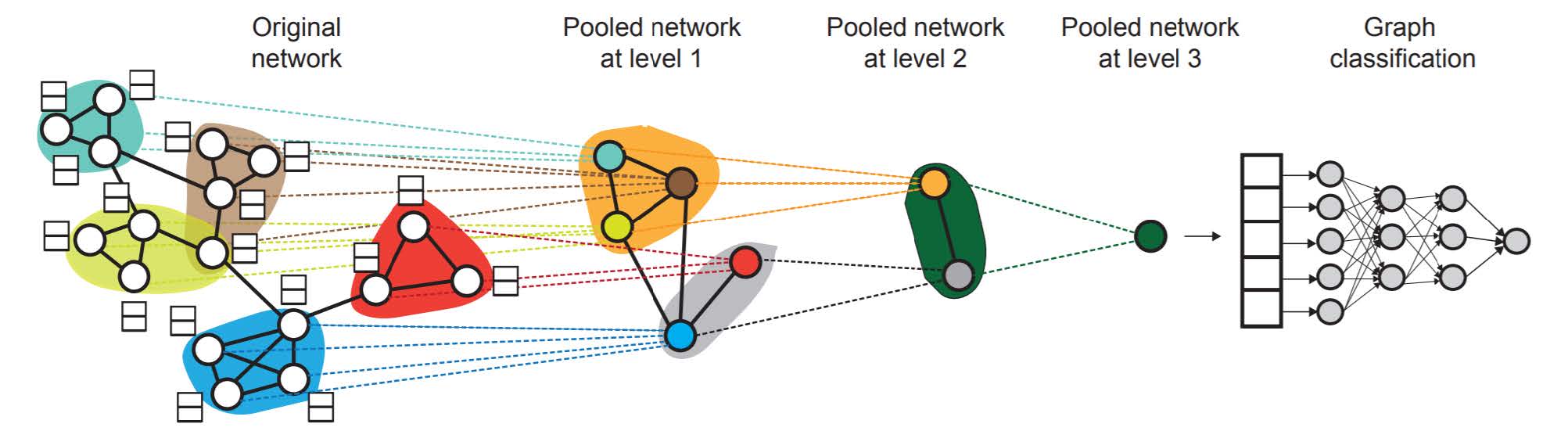
# 嵌入的应用

这部分直接搬运 sildes, 写得非常好：

• 聚类 / 集群探索 (Clustering/community detection): 将嵌入 $\boldsymbol{z}_i$ 进行聚类。
• 节点分类 (Node classification): 基于嵌入 $\boldsymbol{z}_i$ 预测节点 $i$ 的标签。
• 链路预测 (Link prediction): 基于嵌入 $(\boldsymbol{z}_i, \boldsymbol{z}_j)$ 预测边 $(i, j)$. 此处可以进行的操作包括：
  • 连接 (Concatenate): $f(\boldsymbol{z}_i, \boldsymbol{z}_j)= g([\boldsymbol{z}_i, \boldsymbol{z}_j])$.
  • 哈达玛积 (Hadamard product): $f(\boldsymbol{z}_i, \boldsymbol{z}_j)= g(\boldsymbol{z}_i * \boldsymbol{z}_j)$.（对应项相乘）
  • 求和 / 求平均 (Sum/Avg): $f(\boldsymbol{z}_i, \boldsymbol{z}_j)= g(\boldsymbol{z}_i + \boldsymbol{z}_j)$.
  • 求距离 (Distance): $f(\boldsymbol{z}_i, \boldsymbol{z}_j)= g(\|\boldsymbol{z}_i . \boldsymbol{z}_j\|_2)$.
• 图分类 (Graph classification): 基于嵌入 $\boldsymbol{z}_i$ 预测图 $G$ 的嵌入 $\boldsymbol{z}_G$, 可以采用前面提到的方法。