# 任务
PageRank 算法是 Google 用于搜索引擎的算法,由两名 Stanford 博士生 Lawrence Page 和 Sergey Brin 在 1998 年提出。首先,我们给出问题的建模。
# 信息网络
网页是一种信息网络,通过超链接实现网页间的有向关系,从而构成一个图。类似地,论文的引用网络、百科全书的参考文献网络也是信息网络。我们要做的就是计算网络上不同节点的重要性排序。
下面,我们将介绍三种算法:
- PageRank
- Personalized PageRank (PPR)
- Random Walk with Restarts
# PageRank
# 想法
PageRank 算法通过链接衡量网页的重要性。注意到,相比于离开链接,进入链接更加难以伪造,因此选择进入链接作为重要性的衡量。假设一个重要性为 的页面 有 个离开链接,那么每一个离开链接都会给 指向的对应节点带来 的重要性,即
其中 是节点 的出度。下面是一个简单的例子:
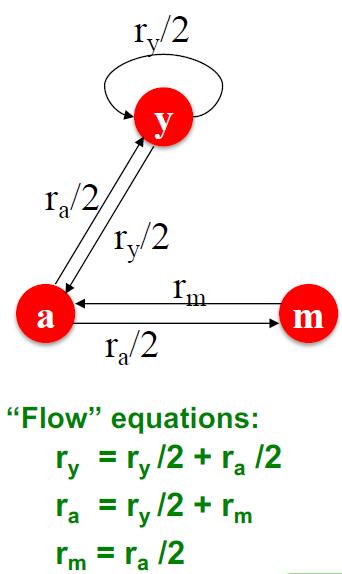
基于上面的例子,添加一个关于值的条件 后可以通过线性方程组求解得到各个节点的重要性。
实际上,我们有更加简单的算法、
# PageRank 的矩阵形式
定义随机邻接矩阵 满足:若节点 有 个出度,, 则 .
因此, 各列和均为 , 可以看作是一个列随机矩阵 (colomn stochastic matrix).
此外,我们将各节点重要性作为坐标组成的向量 称为排名向量 (rank vector), 其满足 , 因此是一个随机分布。
所以 rank vector 是这么翻译吗?I'm not sure...
注意到(和之前提到的特征向量中心性有些类似)
该描述与前面的方程组是等价的,但更加简洁。
此外,对于该表示我们还从随机游走的角度理解。假如一个网页浏览者在 时刻到达一个网页,那么他会在 时刻离开,并随机选择下一个网页。因此,我们可以表示为
这样的 Markov 链是存在平稳分布 (Stationary Distribution) 的,即条件 .
# 计算
# 幂法
下面的问题是,如何计算 的解。在这里,我们采用数值分析的幂法求解。包括以下步骤:
- 初始化:.
- 迭代:.
- 停止:当 时停止。
一般情况下,采用 次迭代可以得到结果。
# 矩阵形式的可靠性
这一算法很简单,但是带来的的问题包括:
- 迭代是收敛的吗?
- 迭代可以得到我们想要的结果吗?
- 结果是合理的吗?
在实际情况中,会出现两种现象导致上述的迭代失效,我们分别称为蜘蛛陷阱 (spider trap) 和死胡同 (dead end).
# 蜘蛛陷阱
蜘蛛陷阱指的是网页浏览者进入一个仅指向内部的子图,导致浏览者无法离开该子图的情况。例如进入一个只有自环的节点。此时,我们的矩阵仍然符合定义,但是得到的结果并不合理。
因此,我们可以考虑将陷入蜘蛛陷阱的浏览者随机传送到图中的任意节点,这样就可以保证浏览者不陷入蜘蛛陷阱。
# 死胡同
死胡同指的是网页浏览者进入一个不指向其它边的节点。此时该节点在矩阵 中对应列为零向量,不符合数学要求。我们同样可以将其按均等概率随机传送到其它节点。
# 改进的矩阵形式
加入随机传送后,我们的重要性表示变为
其中 是超参数,表示不进行随机传送的概率, 是图中的节点总数。
该表示对应的矩阵形式为
其中, 表示一个各项均为 的矩阵,即随机传送矩阵。另外,此处的 是 Google 的含义。
此时,我们采用幂法进行 迭代,即可得到想要的解。
需要注意的是, 的值严重影响结果的合理性。因此需要审慎选择超参数。
# 个性化 PageRank 和带有重启的随机游走
# 任务:推荐算法
在这里,我们考虑一个新的任务,作为两个算法的引入。该任务就是经典的推荐问题。
推荐问题本身可以建模为一个二分图 (bipartite graph), 其中的两类节点分别表示用户和物品,二分图中的边代表用户对物品的交互,例如点击、购买等操作。我们希望基于用户的交互,为用户推荐与先前交互相似的物品。这个任务称为图上的接近性衡量 (proximity on graph).
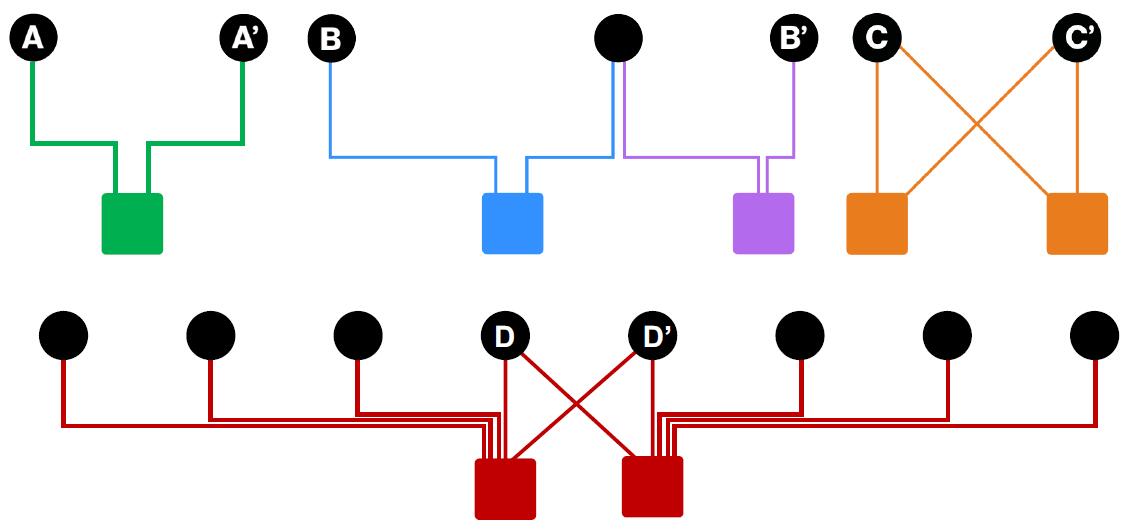
例如,上图中 与 的相似程度高于 与 , 这是因为 与 之间的路径更短。
此外, 与 的相似程度高于 与 , 这是因为 与 具有更多的共同用户。
但注意到, 与 之间的相似度低于 与 , 因为 与 的共同用户都具有更广泛的交互,因此更难有把握说两者相似度更高。
# 算法对比
PageRank, Personalized PageRank 和 Random Walk with Restarts 的差别仅在于传送集 (teleportation set) 的不同。
- PageRank: , 即可以随机传送到所有节点。
- Personalized PageRank: 可以传送到某一个固定的节点集 .
- Random Walk with Restarts: , 即只能随机传送到特定节点 . 这可以看作是返回随机游走的起点,因此得名。
# 算法有效性分析
为什么 PageRank 及其相关算法如此有效?基于上述推荐的例子,该算法在多个方面对相似度进行了衡量,包括
- multiple connections: 更多的共同邻居 / 连边意味着更大的相似度
- multiple paths: 更多的相连路径也意味着更大的相似程度
- direct & indirect paths: 直接相关和间接相关的节点具有不同的相似度。
- Degree of the node: 度更多的节点在推荐中提供的相似可信度更低。
我们发现,PageRank 算法思路可以体现上述相似度的衡量。
# 矩阵分解与节点嵌入
在这一小节中,我们将简单说说矩阵分解和节点嵌入的关系。
# 嵌入矩阵
定义嵌入矩阵 , 其中 是嵌入维度, 是节点数量。在该矩阵中,每个节点的嵌入是矩阵的一列。如果两个节点更加相似,那么对应列的点积则更大。
# 连边相似的矩阵分解
现在考虑一种简单的相似性假设:如果两个节点 之间有边相连,那么认为两个节点是相似的。此时有 . 则对于矩阵 , 其应该满足
注意到,, 因此上述表示不可能严格取等号(也就是说嵌入过程是出现信息丢失的)。因此,我们只需要求解一个近似的嵌入矩阵 即可。即对于给定嵌入维度 , 求
这里采用的范数是 norm (Frobenius norm).
# 基于随机游走相似性的矩阵分解
DeepWalk 算法和 node2vec 算法都是基于随机游走的相似性假设。该假设中,若两节点处于同一随机游走路径中,则两节点更加相似。
这一数学框架是在 Network Embedding as Matrix Factorization: Unifying DeepWalk, LINE, PTE, and node2vec 文章中提出的。这篇文章值得一看。
对于 DeepWalk 算法,其求解等价于分解如下表达的矩阵
其中,, 是随机游走窗口大小, 是负采样的样本数。
# 基于随机游走算法的缺陷
基于随机游走的算法有如下缺陷:
- 不能对不在训练集中的节点进行嵌入,这意味着如果节点随时间增加,那么新增的节点无法处理。
- 不能捕获结构的相似性,例如下图中标号为
1和标号为11的节点位于相似的结构中,但是由于节点1为起始节点,其嵌入会完全不同。但基于匿名随机游走的方法可以解决这一问题。 - 分割了节点、边和图的关联。实际上我们只能创建节点嵌入,但边和图的信息无法整合进入框架中。
