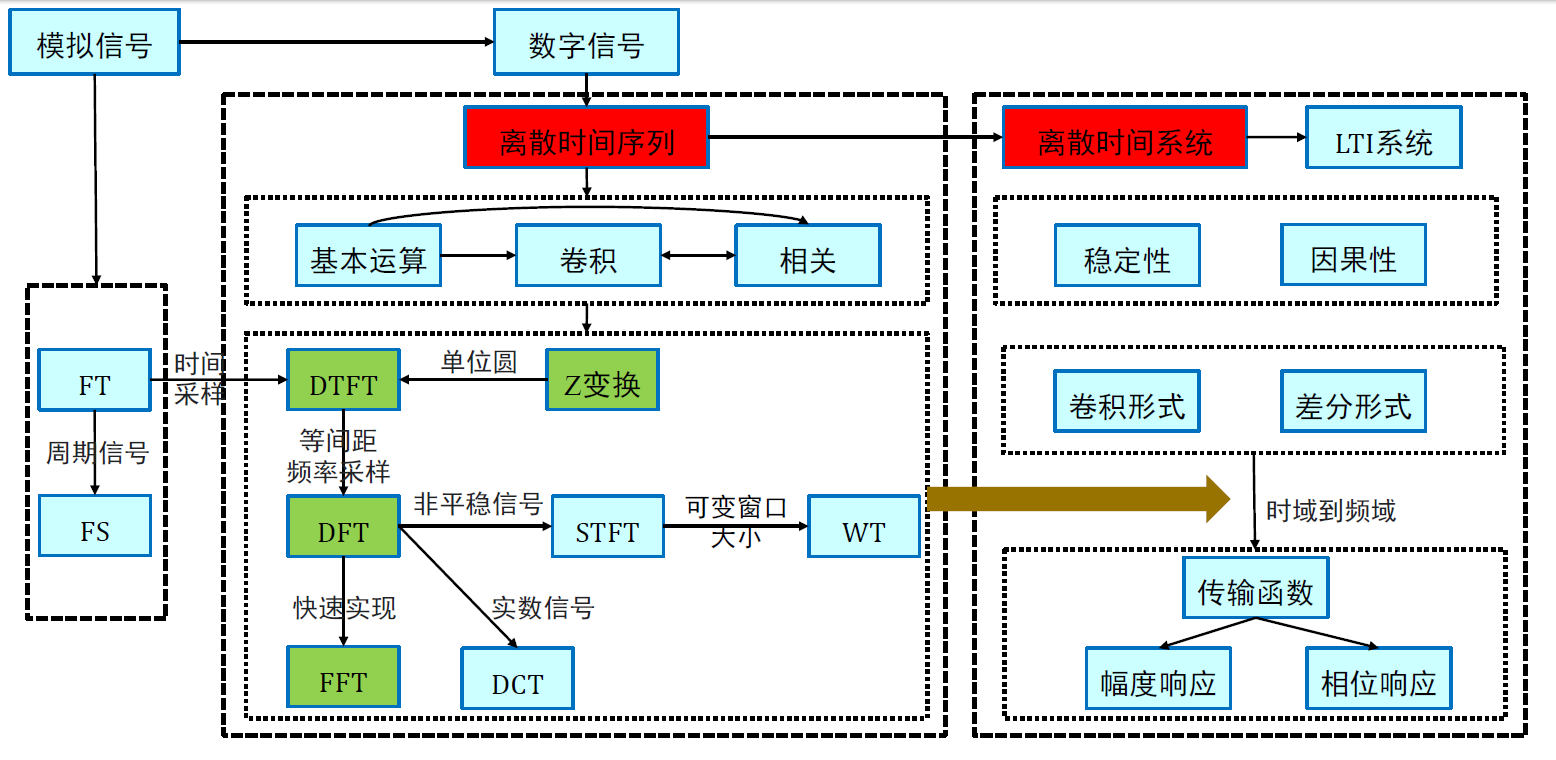
给人工智能专业学生的数字信号处理课程。

# 信号

A Signal is a function that "conveys information about the behavior or attributes of some phenomenon."

信号是传递某些现象的行为或属性的信息的函数。

对于一维时间信号，定义时间坐标为 $t \in \mathbb{R}$, 则信号可以表示为一个关于时间的函数 $f(t)$ 满足

$$f: \mathbb{R} \to \mathbb{R}.$$

对于一个时空信号，空间坐标为 $\vec{\bm{r}} = (x,y,z) \in \mathbb{R}^3$, 则信号可以表示为一个关于时间和空间的函数 $f(\vec{\bm{r}}, t)$ 满足

$$f: \mathbb{R}^3 \times \mathbb{R} \to \mathbb{R}.$$

# 数字信号与模拟信号

# 概念

模拟信号是自然界中直接采集的信号，是一个连续函数。数字信号则是一组有限离散的数字序列，可以直接存储在存储介质中。我们一般用小括号 $x(t)$ 表示模拟信号即自变量连续的信号，用方括号 $x[n]$ 表示数字信号等自变量离散的信号。

# 对比

1. 数字信号是离散的，模拟信号是连续的
2. 各种数字信号可以在同一介质上存储，不同的模拟信号需要不同的存储介质

# 转换

模拟信号转换为数字信号包括两个步骤：

1. 量化：确定信号强度的离散幅度
2. 采样：确定离散时间的间隔

# 香农 - 奈奎斯特定理 (Shannon-Nyquist theorem)

如果一个函数 $x(t)$ 没有高于 $B$ 赫兹的频率，那么它可以从其在一系列点上的函数值完全确定，这些点相隔小于 $T_s=1/2B$ 秒。精确地，有以下等式成立：

$$x(t) = \sum_{n=-\infty}^{+\infty}x[n] \frac{\sin\left(\pi(t-nT_s)/T_s\right)}{\pi(t-nT_s)/T_s}.$$