LDA 的 MATLAB 实现。

# Experiment 3: Linear Discriminant Analysis

This is a report on Experiment 3: Linear Discriminant Analysis.

# Purpose

In this experiment, we want to reduce the dimension of some datasets with a supervised method, the LDA algorithm.

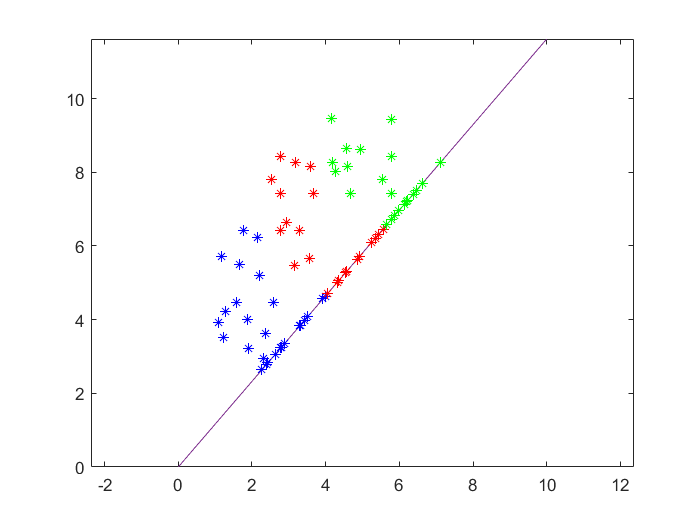
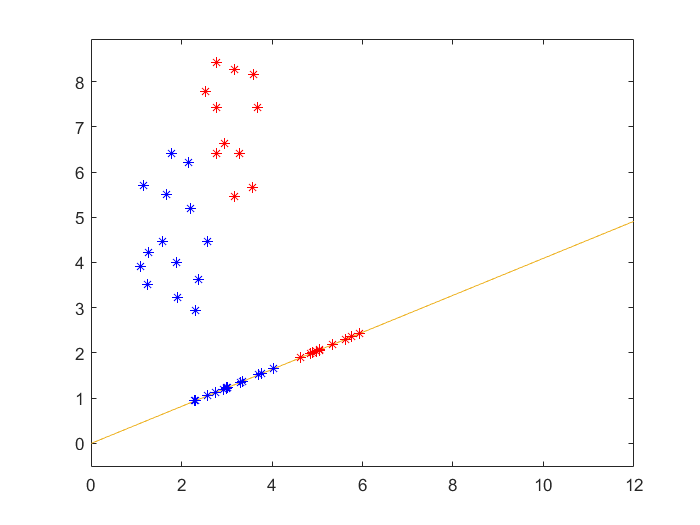
Two datasets are given; the first has two categories, and the second one has three categories.

# Hypothesis

We assume that the pre-marking is correct.

# Procedure

For the dataset with two categories, I first calculated the between-class scatter $S_b = (\mu_1 - \mu_2)(\mu_1 - \mu_2)^\top$ and the within-class scatter$S_w = \sum_{i=1}^2\sum_{x \in C_i}(x-\mu_i)(x-\mu_i)^\top$.

The cost function is defined as

$$\min_\theta J(\theta) = -\theta^\top S_b\theta + \lambda(\theta^\top S_w \theta - 1)$$

in which $\lambda$ is a Lagrange multiplier. Without loss of generality, we set $\theta^\top S_w\theta = 1$. Then we know that $\theta^*$ is the eigenvector of $S_w^\top S_b$ corresponding to the maximum of eigenvalue.

After that, we draw the points projected onto the line $y = \theta^*x$.

For the dataset with three categories, the calculation is the same.

# Results

The diagram of the dataset with two categories is as follows:

The diagram of the dataset with three categories is as follows: