采用牛顿法求解对数概率回归模型。

# Experiment 4: Logistic Regression and Newton's Method

This is the report of Experiment 4: Logistic Regression and Newton's Method.

# Purpose

In this experiment, we want to implement logistic regression on a classification problem.

The value of inputs $\{x^{(i)}\}$ are each students' score on two standardized exams. The value of $\{y^{(i)}\}$ is a label of whether the student was admitted.

# Hypothesis

We hypothesize that there exists $k$ that for each $i$, the probability can be written as $P(x^{(i)}_1 + kx^{(i)}_2)$.

# Procedure

The predict question is a classification problem.With the hypothesis, we want to divide all data points into two groups by a line, the positive group is the students were admitted, the negative group is the students were not admitted. Now, I'll find the line with Newton's Method.

We predict the possibility with the hypothesis function

$$h_\theta(x):=g(\theta^\top x) = \frac{1}{1+e^{-\theta^\top x}} = \mathbb{P}(y=1\|x;\theta)$$

Through maximum likelihood estimation, the logarithm of likelihood function $J(\theta)$ is

$$J(\theta) := -\frac{1}{m}\sum_{i=1}^m\left(y^{(i)} \log\left(h_{\theta}(x^{(i)})\right) + (1-y^{(i)})\log\left(1-h_{\theta}(x^{(i)})\right)\right)$$

We want to minimize the function with Newton's method, whose update rule is

$$\theta^{(t+1)} = \theta^{(t)} - H^{-1}\nabla_\theta J$$

The gradient $\nabla_\theta J$ is

$$\frac{1}{m}\sum_{i=1}^m\left(h_{\theta}(x^{(i)})-y^{(i)}\right)x^{(i)}$$

The inverse of Hessian $H^{-1}$ is

$$H^{-1} = \frac{1}{m}\sum_{i=1}^mx^{(i)}{x^{(i)}}^\top\left(h_\theta(x^{(i)})\right)\left(1-h_\theta(x^{(i)}\right)$$

So we can calculate the $\hat\theta$ with Newton's method. After convergence, we need to draw the decision boundary of this classification problem. The line satisfies that

$$\mathbb{P}(y=1|x;\theta) = h_{\theta}(x) = 0.5$$

which means

$$\theta^\top x = 0$$

# Answer of the questions

# Question 1

After $5$ iterations, I got the $\theta$ is

$$\theta = (-16.378740, 0.148341, 0.158908)^\top$$

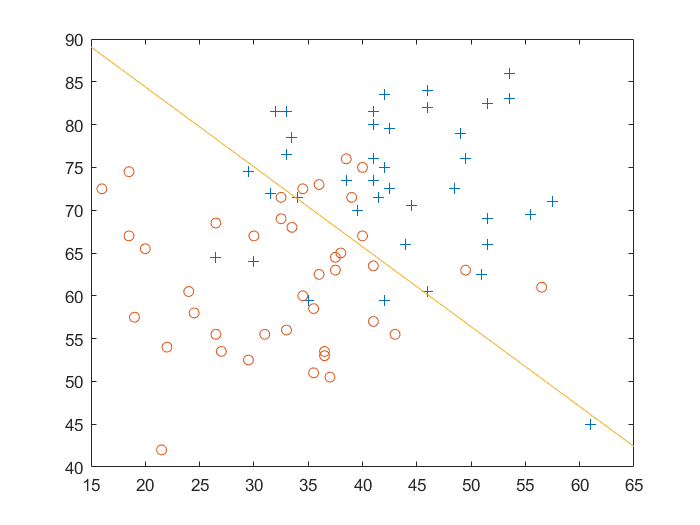
# Question 2

The probability that a student with a score of $20$ on Exam 1 and a score of $80$ on Exam 2 is $0.331978$.