# 概述

# 概念

决策树 (decision tree) 是一种用于分类算法的树形结构。树的根节点是数据集全体，每个内部节点是一个判断语句，每个叶子节点是最终的一种分类。例如，下图是一个简单的决策树：

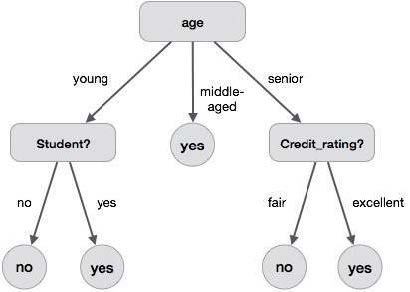
# 特点

决策树算法是一种监督学习算法，其不能发现数据集中的潜在特征，只能将数据集按其提供的特征进行分类。

# 评价

评价一个决策树的好坏，关键看起泛化误差的大小，即其在总体数据集上的分类效果。

# 复杂度和算法思路

已经证明，在一个训练集上寻找一个最优决策树是 NP-hard 的 (Hancock et al., 1996). 因此，生成决策树的算法大多是启发式的贪心算法。

# 特征选取准则

决策树依照特征分类。其特征选取有一些准则，作为决策树可解释性和分类效果的体现。

对离散特征，其可以进行二分类，也可以进行多分类。分类方式依靠具体算法的实现。

对有序特征，分类时需要保持特征的顺序。

# 决策树生成算法

决策树的经典算法包括 ID3(1986), C4.5(1993), C5.0, CART (Classification and Regression Trees, 1984) 等。

# ID3

经典的二分类算法，其规则如下：

• 若该节点处带分类集合 $S$ 中所有元素属于同一类 $C$, 则将该节点视作一个标注 $C$ 的叶节点。
• 采用某些启发式函数 (如信息增益) 进行分类。

# 信息熵和信息增益

对一个有分类数据集 $S$, 熵 (Entropy) 定义为

$$E(S):=-\sum_c p_c \log_2 p_c$$

其中 $c$ 是 $S$ 中的各类别。(可以补充定义 $0\log 0 = 0$. )

熵越大，代表数据越混乱，分类效果越差。

# C4.5