首页 计算机 机器学习 经典模型

这篇笔记是对 Attention Is All You Need 文章的总结。

# 概述

Transformer 起初被设计为一种面向机器翻译任务的序列转录模型 (sequence reansduction models). 不同于先前的基于 RNN 或 CNN 的模型，Transformer 模型是完全基于注意力机制的模型，不需要递归和卷积。基于实验结果，Transformer 模型具有更高的质量和更高的并行性。

# 序列转录问题

序列转录问题是输入和输出都为序列的问题，包括语音识别、文本转语音、机器翻译、蛋白质二级结构预测 (protein secondary structure prediction) 等等。不那么显然的是，图灵机的执行也可以看作一种序列转录。

先前的序列转录模型中，表现最好的是依赖注意力机制连接编码器和解码器。Transformer 也不例外，仍然是 encoder-decoder 架构。

# 模型架构

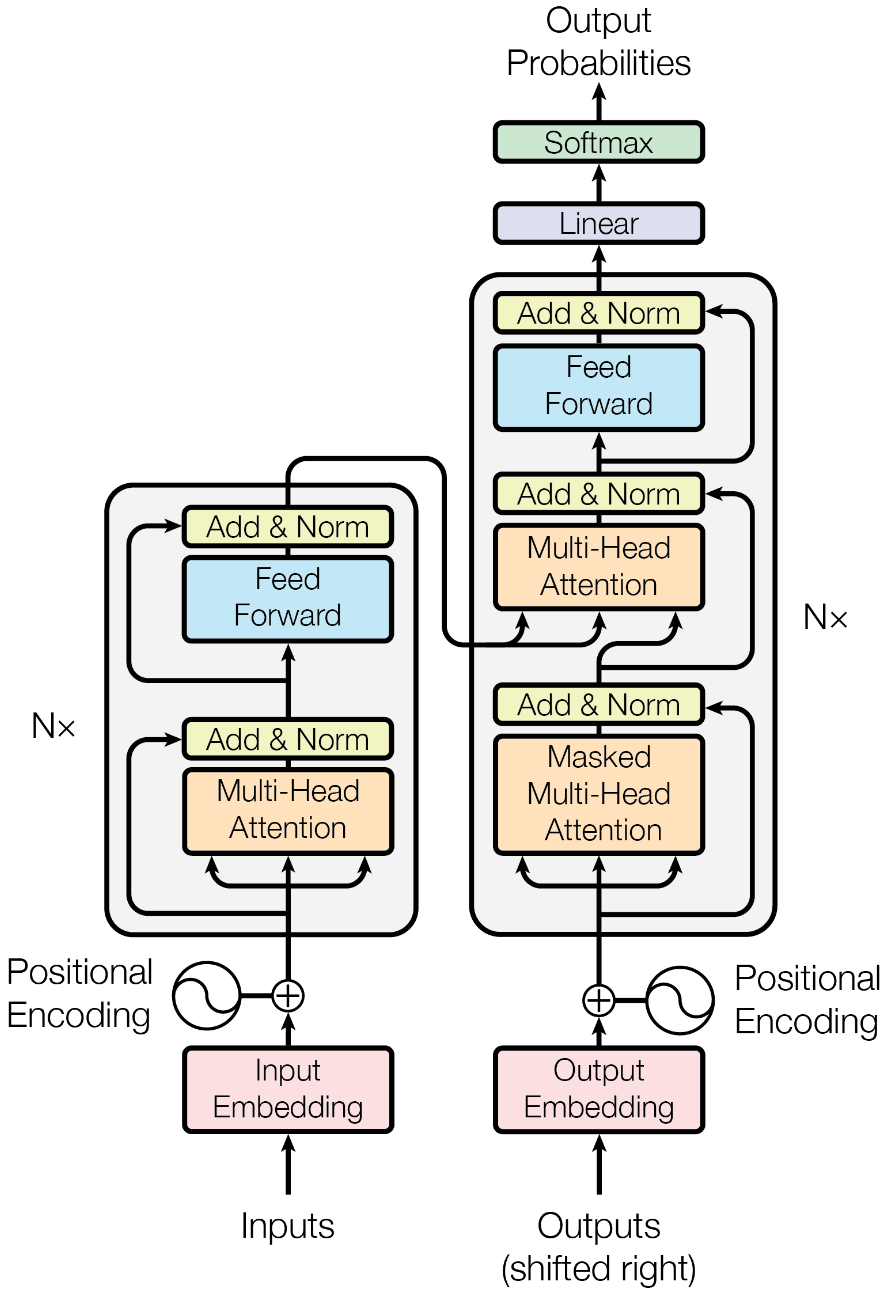
# encoder-decoder 架构

序列转录问题就是将输入序列 x=(x1,x2,…,xn)\boldsymbol{x} = (x_1, x_2, \dots, x_n) 转化为输出序列 y=(y1,y2,…,ym)\boldsymbol{y} = (y_1, y_2, \dots, y_m) 的问题。在 encoder-decoder 架构中，encoder 负责将输入序列 x\boldsymbol{x} 转化为一个与输入向量长度相同的向量 z=(z1,z2,…,zn)\boldsymbol{z} = (z_1, z_2, \dots, z_n), decoder 负责将这个向量转化为输出序列 y\boldsymbol{y}.

# 注意力机制

注意力机制 (attention mechanisms) 并不是 Transformer 模型首创的。实际上，注意力机制此前已经在 encoder-decoder 架构中多次使用了。

注意力机制是一种用于计算两个序列之间的相关性的方法。在 encoder-decoder 架构中，注意力机制被用于计算输入序列和输出序列之间的相关性，用来将 encoder 生成的内容高效传递给 decoder.

# 任务

注意力模型的输入是一个 query qq 和一些 key-value 对 (ki,vi)(k_i, v_i), 输出 output oio_i 是一个 value 的加权平均。其中各 value 的权重通过 query 与各 key 的相似度确定。

# Scaled Dot-Product Attention

Transformer 中采用缩放的点乘注意力机制 (scaled dot-product attention) 作为具体实现，这实际上是一种最简单的注意力机制。

在这样的注意力机制中，存在一个假设：query qq 与 key kik_i 的维度相同，在这里假设为 dkd_k. 因此，相似度 q⋅kiq \cdot k_i 可以直接通过点积计算得到，这就是 dot-product 的含义。此后，基于 query & key 的长度，将结果除以 dk\sqrt{d_k} 进行归一化，然后放入 softmax 函数中，就得到了第 ii 个 value 的权重。也即

Attention(q,ki,vi)=softmax(q⋅kidk)vi=exp⁡(q⋅ki/dk)∑jexp⁡(q⋅kj/dk)vi.\mathrm{Attention}(q, k_i, v_i) = \mathrm{softmax} \left(\frac{q \cdot k_i}{\sqrt{d_k}}\right) v_i = \frac{\exp(q \cdot k_i / \sqrt{d_k})}{\sum_j \exp(q \cdot k_j / \sqrt{d_k})} v_i.

显然，这一过程可以直接采用矩阵表示：

Attention(Q,K,V)=softmax(QK⊤dk)V.\mathrm{Attention}(Q, K, V) = \mathrm{softmax} \left(\frac{Q K^\top}{\sqrt{d_k}}\right) V.

这也就是 Transformer 可以并行的一个原因。

为什么要除以 dk\sqrt{d_k}?

基于文章解释，点乘中的项 qi,kiq_i, k_i 都是均值为 00 且方差为 11 的，因此将 q⋅k=∑i=1dkqikiq \cdot k = \sum_{i=1}^{d_k} q_ik_i 进行方差归一化需要除以 dk\sqrt{d_k}.

下图就是 Scaled Dot-Product Attention 的示意图：

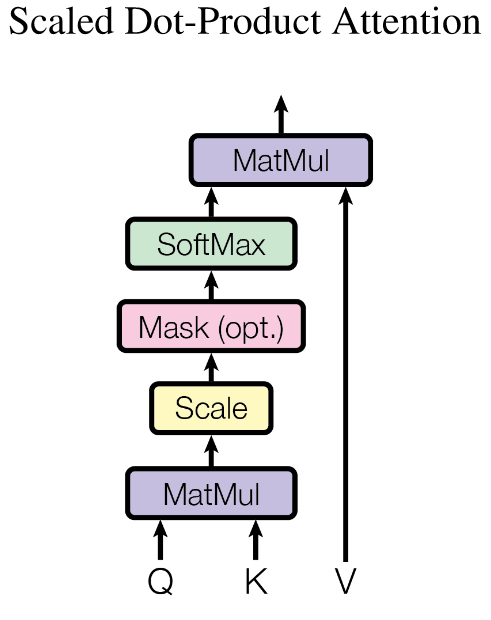
# mask

模型中一个特殊的模块是掩码模块 Musk(opt.) . 其作用是遮盖掉生成项之后的值，以防止模型在生成过程中使用这些值。注意到，由于 decoder 的目标是生成，而 encoder 的目标是将数据集进行特征提取，因此只需要在 decoder 中使用 mask.

这里的掩码 Mask 放在 softmax 前，实现的方式如下：

在 QK⊤Q K^\top 时，显然靠前的 query 也可以与后面的 key 进行交互。于是对 query 之后的 key 对应内积变为一个非常大的负值 (例如 -1e10 ), 这样在 softmax\mathrm{softmax} 之后这些项的权重就会变成 00, 同时在 softmax\mathrm{softmax} 前使用 mask 可以保证权重的归一化。

训练和预测过程中，mask 恒生效。

# Multi-Head Attention

文章中提出的多头注意力 (multi-head attention) 实际上是将 Q,K,VQ, K, V 多次投影到低维向量，分别学习的方法。用公式可以表示为

MultiHead(Q,K,V)=Concat(head1,…,headh)WO,whereheadi=Attention(QWiQ,KWiK,VWiV).\begin{aligned} & \mathrm{MultiHead}(Q, K, V) = \mathrm{Concat}(\mathrm{head}_1, \dots, \mathrm{head}_h) W^O, \\ & \qquad \text{where} \; \mathrm{head}_i = \mathrm{Attention}(QW_i^Q, KW_i^K, VW_i^V). \end{aligned}

其中，WiQ∈Rdmodel×dk,WiK∈Rdmodel×dk,WiV∈Rdmodel×dvW_i^Q \in \mathbb{R}^{d_{\mathrm{model}} \times d_k}, W_i^K \in \mathbb{R}^{d_{\mathrm{model}} \times d_k}, W_i^V \in \mathbb{R}^{d_{\mathrm{model}} \times d_v} 是对应向量的投影矩阵。WO∈Rhdv×dmodelW^O \in \mathbb{R}^{hd_v \times d_{\mathrm{model}}} 是映射回原空间的投影矩阵。

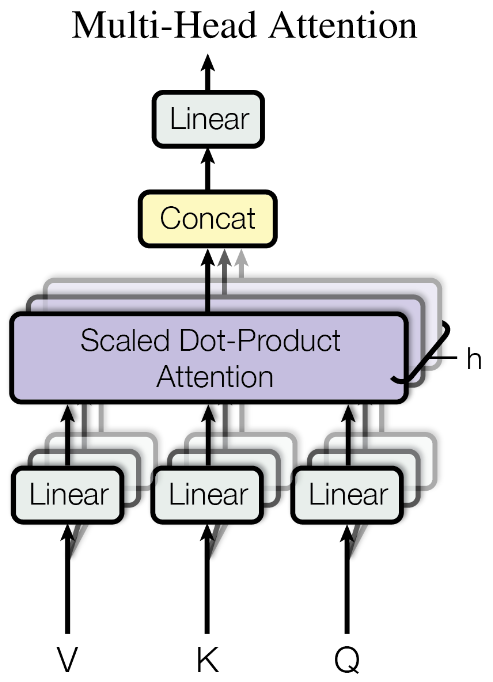
在 Transformer 中，取头数 h=8h = 8, 这样 dk=dv=dmodel/h=64d_k = d_v = d_{\mathrm{model}}/h = 64.

设计多头注意力的一个重要原因是前面所说的基本的点积注意力机制是不存在学习参数的，而这里的低维映射矩阵是可学习的。我们希望增大模型可学习的参数数目，从而模型可以更好适应不同的任务。

# Transformer 中的注意力模块

重新观察 Transformer 模型。其总共包括三个注意力模块：

  • encoder 部分的多头自注意力模块：这一模块的输入 q,k,vq, k, v 均相同，是输入序列的一个线性变换，用来学习输入序列的内在特征。
  • decoder 部分的掩码多头自注意力模块：该模块的作用同样是基于输入生成的 token 序列，学习其内在特征。类似 encoder 中的自注意力模块，同样需要输入均相同。这里加入掩码，是希望借助掩码来控制 decoder 中的自注意力模块，使其只能关注到之前已经生成的 token 上。
  • decoder 部分的 encoder-decoder 注意力模块：该模块较特殊，其输入 qq 来自 decoder 中的前一个 token，而 k,vk, v 来自 encoder 中的输出。这样，该模块可以将 encoder 中提取的特征传递到 decoder 中。

# Ref

  • encoder-decoder 部分：
    • 拆 Transformer 系列一：Encoder-Decoder 模型架构详解 - 随时学丫 - 知乎
  • The Illustrated Transformer - The Illustrated Transformer