# 复数

# 复数的表示形式

# 代数形式

复数的最基本的表示为代数形式，即

$z = a + bi, \quad a,b \in \mathbb{R}$

其中 $a\triangleq\mathrm{Re}z$ , 称为实部， $b\triangleq\mathrm{Im}z$ , 称为虚部。将 $a,b$ 分别视为二维坐标系中的横纵坐标，就得到了一个用来表示复数的平面，称为复平面。

# 三角形式

对于二维平面，除了采用平面直角坐标表示，另一种常见的方式就是采用极坐标进行表示。对应到复数上，就是复数的三角形式，即

$z = r (\cos \theta + i \sin \theta),\quad r \in [0,\infty), \, \theta \in \mathbb{R}$

这时候，用三角恒等式可以得到一个三角形式下复数的乘法公式，称之为棣莫弗公式 (de Moivre's formula), 即

$(\cos x + i\sin x)^n = \cos nx + i \sin nx$

于是可以看出，复数相乘，则幅角相加。在实数范围内，对于此性质，我们求解函数方程可以得到其对应的是指数的形式。于是自然可以联想到复数可以采用指数进行表示。此时可以暂且引入一个复数的简化表示形式，称为复数的指数形式，即

$z = r (\cos \theta + i\sin \theta) \triangleq r e^{i\theta}$

# 球面表示

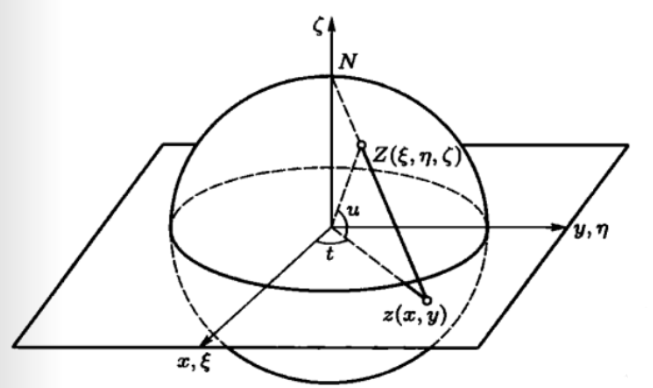
此外，借助于球极投影，我们还可以得到复数的球面表示。

对于单位球上的一点 $Z(\xi, \eta, \zeta)$ , 容易得到其与复平面上点 $z(x,y)$ 之间的对应关系为

$\xi = \frac{2x}{1+|z|^2},\; \eta = \frac{2y}{1+|z|^2},\; \zeta = \frac{|z|^2-1}{1+|z|^2}$

以及

$x = \frac{\xi}{1-\zeta},\; y = \frac{\eta}{1-\zeta}$

我们称 $(\xi,\eta,\zeta)$ 这种表示为复数的球面表示。此时，点 $(0,0,1)$ 不表示复平面上的某个点，而是表示复平面上无穷远的点。因此，复数的球面表示可以让无穷远点也有一个良好的表示方式。此时，我们称包括了无穷远点的复数集为扩充复数集，记作 $\mathbb{C}_\infty$ 或 $\bar{\mathbb{C}}$ . 在 $\bar{\mathbb{C}}$ 上也可以以球面上两点的欧氏距离定义度量，称为球面度量.

# 复变函数的概念

对定义域 $E\subseteq\mathbb{C}$ , (单) 复变函数是一个映射 $f: E \to \mathbb{C}$ , 即函数是单值的。多复变函数是一个 $E \to 2^\mathbb{C}$ 的映射，即函数是多值的。

如果采用代数形式看复变函数，那么其可以简单分解为两个实值函数的组合。即 $w=f(z) = \mathrm{Re}f(z) + \mathrm{Im}f(z) = u(x,y) + iv(x,y)$ .

我们可以从拓扑的视角看复变函数，因为复变函数是一个平面到平面的变换。