首页 数学 概率论

时光只解催人老，不信多情，长恨离亭，泪滴春衫酒易醒。

# 概率空间

概率论的基本研究范围是概率空间。因此，首先需要完成的任务是将概率空间的定义进行严谨化、公理化。

关于概率，我们有一些朴素的、未加证明的结论。最常见的三者为古典概型、几何概型及频率接近于概率。以此为基础的猜想方向，我们可以进行概率的公理化。

首先，我们需要一些测度论的基础知识。

# 预备知识

设 Ω\Omega 是一个非空集合，其中的元素称为点，用 ω\omega 表示。我们考虑 Ω\Omega 的子集组成的一个集类 F\mathscr{F}. 并考虑以下的几个性质：

  1. E∈F⇒Eˉ∈FE \in \mathscr F ⇒ \bar E \in \mathscr F
  2. E1,E2∈F⇒E1∪E2∈FE_1,E_2 \in \mathscr F ⇒ E_1\cup E_2 \in \mathscr F
  3. E1,E2∈F⇒E1∩E2∈FE_1,E_2 \in \mathscr F ⇒ E_1\cap E_2 \in \mathscr F
  4. ∀n≥2:Ei∈F,1≤i≤n⇒∪i=1nEi∈F\forall n \geq 2:\,E_i \in \mathscr F,\,1\leq i\leq n ⇒ \cup_{i=1}^nE_i \in \mathscr F
  5. ∀n≥2:Ei∈F,1≤i≤n⇒∩i=1nEi∈F\forall n \geq 2:\,E_i \in \mathscr F,\,1\leq i\leq n ⇒ \cap_{i=1}^nE_i \in \mathscr F

# 条件概率与独立性

# 条件概率

设 (Ω,F,P)(\Omega, \mathscr{F}, P) 是一个概率空间，B∈FB \in \mathscr{F}, P(B)>0P(B) > 0, 则 ∀A∈F\forall A \in \mathscr{F}, 记

P(A∣B)≔P(AB)P(B)P(A|B) \coloneqq \frac{P(AB)}{P(B)}

称其为在某事件 BB 发生的条件下，事件 AA 发生的条件概率 (conditional probability)。

基于上述定义，立刻可以得到

P(AB)=P(B)P(A∣B)P(AB) = P(B) P(A|B)

该式称为概率的乘法公式。

下面给出一个条件概率的例子。

在肝癌普查中发现，某地区的自然人群中，每十万人内平均有 40 人患原发性肝癌，有 34 人甲胎球蛋白高含量，有 32 人既患原发性肝癌又出现甲胎球蛋白高含量。

将某人患原发性肝癌事件记作 CC, 某人甲胎球蛋白高含量事件记作 DD, 则

P(D∣C)=P(CD)P(C)=3.2×10−44×10−4=0.8P(C∣D)=P(CD)P(D)=3.2×10−43.4×10−4=0.9412P(D|C) = \frac{P(CD)}{P(C)} = \frac{3.2 \times 10^{-4}}{4 \times 10^{-4}} = 0.8 \\ P(C|D) = \frac{P(CD)}{P(D)} = \frac{3.2 \times 10^{-4}}{3.4 \times 10^{-4}} = 0.9412

因此，DD 事件发生使得 CC 发生的概率从 4×10−44 \times 10^{-4} 升高到了 0.94120.9412, 即条件（信息）可以影响事件的发生概率。

# 混淆矩阵

将上面的例子一般化，就得到了混淆矩阵，这是对一个正负分类器的重要评价方式。

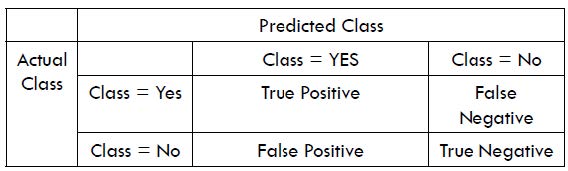
一个混淆矩阵中各项如下：

其中各项含义如下：

  • 条件阳性 (Condition Positive, P): 即样本中的正样例数量。
  • 条件阴性 (Condition Negative, N): 即样本中的负样例数量。
  • 真阳性 (True Positive, TP): 分类器正确分类为正的样例数量。
  • 真阴性 (True Negative, TN): 分类器正确分类为负的样例数量。
  • 假阳性 (False Positive, FP): 又称第一类错误 (Type I Error), 表示分类器错误预测为正样例的情况。
  • 假阴性 (False Negative, FN): 又称第二类错误 (Type II Error), 表示分类器错误预测为负样例的情况。

基于以上各项，我们可以定义一些评价指标：

  • 准确率 (accuracy) 定义为

    ACC=TP+FPTP+TN+FP+FN\mathrm{ACC} = \frac{\mathrm{TP} + \mathrm{FP}}{\mathrm{TP+TN+FP+FN}}

  • 真阳性率 (True Positive Rate, TPR), 又称灵敏度 (sensitivity rate)、召回率 (recall rate)、查全率 (hit rate)。定义为

    TPR=TPP=TPTP+FN=1−FNR\mathrm{TPR} = \frac{\mathrm{TP}}{\mathrm{P}} = \frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FN}} = 1 - \mathrm{FNR}

  • 阳性预测率 (Positive Predictive Value, PPV), 又称精准率 (precision value)、查准率。定义为

    PPV=TPTP+FP=1−FDR\mathrm{PPV} = \frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FP}} = 1 - \mathrm{FDR}

  • F1F_1 值 (F1F_1 measure) 是查准率与查全率的调和平均：

    F1=2×TPR×PPVTPR+PPVF_1 = \frac{2 \times \mathrm{TPR} \times \mathrm{PPV}}{\mathrm{TPR} + \mathrm{PPV}}

# 全概率公式

若事件 {Ai}i=1∞\{A_i\}_{i=1}^\infty 是样本空间 Ω\Omega 的一个分割，即诸 AiA_i 两两不相容，且 ∑i=1∞Ai=Ω\sum_{i=1}^\infty A_i = \Omega, 那么

P(B)=∑i=1∞P(Ai)P(B∣Ai)P(B) = \sum_{i=1}^\infty P(A_i) P(B|A_i)

称为全概率公式 (low of total ability)。可以看出，全概率公式实际上是分类讨论的形式化表述。

# 贝叶斯公式

# 应用

  • 郑瀚 Andrew: 概率图模型（PGM）：贝叶斯网（Bayesian network）初探
  • Bayesian network 与 python 概率编程实战入门
  • VAE