僧衫吹，月如雪，花下已千年。

# 概述

单变元方程求近似解是数值分析最基本、最重要的问题之一，最基本的方法是二分法、不动点迭代法和牛顿法。

# 二分法

# 算法实现和注意事项

二分法 (Bisection Method) 是基于介值定理的基本方法，采用二分区间方式对解的范围减半收缩，代码如下：

//input: function f(x); endpoints: a, b; tolerance TOL; maximum number of iterations N

//output: approximate solution p or message of failure

double FA = f(a);

for (int i = 1; i <= N; i++){

    double p = a + (b-a)/2;

    double FP = f(p);

    if (FP == 0 || (b-a)/2 < TOL) return p;

    if (sgn(FA) == sgn(FP)) a = p;

    else b = p;

}

return p;

其中， sgn(x) = (x>0) ? 1 : ((x<0) ? -1 : 0) 是符号函数。

# 算法中的误差控制

在二分法的代码中，存在一些算法上的误差控制。

首先，在迭代过程中，求 $[a_n,b_n]$ 中点需要采用 $p_n = a_n + (b_n-a_n)/2$ 而非 $p_n = (a_n + b_n)/2$.

此外还要注意，代码中的 sgn(FA)==sgn(FP) 尽量不采用 FA*FP>0 代替，因 FA*FP 可能造成乘法上溢 (但可以采用 sgn(FA)*sgn(FP)<0 代替)。

# 停机控制条件

此外，算法中的停机还可以采用下面的控制条件：

1. $|p_n-p_{n-1}|<\varepsilon$
2. $\displaystyle\frac{|p_n-p_{n-1}|}{|p_n|}<\varepsilon$
3. $|f(p_n)|<\varepsilon$

停机的控制条件是根据实际情况确定的。其中，条件 3 尽量不要使用，因为可能出现 $f(p)$ 的绝对值小，但 $p$ 与零点较远的情况。

# 收敛速度分析

根据二分法的定义，可以证明二分法是线性收敛的。但严谨的证明也不十分容易。

# 不动点迭代

# 基本概念和问题转化

在介绍不动点迭代的方法前，我们先给出不动点的定义：

对于函数 $f(x)$, 若 $\exists p$ 使得 $f(x^\star) = x^\star$, 则称 $x^\star$ 是 $f(x)$ 的不动点 (fixed point).

于是，不动点迭代法 (fixed point iteration) 就是在不动点收敛的前提下，根据反复迭代产生一个收敛序列 $\{x_n\}_{n=0}^{\infty}$, 使得

$$\lim_{n \to \infty}f(x_n) = \lim_{n \to \infty}x_{n+1} = \lim_{n \to \infty}x_{n},$$

从而 $\lim_{n \to \infty}x_{n} = x^\star$, 即求得不动点。

如果需要求解的方程不是 $f(x) = x$ 的形式，而是 $f(x) = 0$ 的形式，那么可以构造 $g(x) = x - f(x)$, 则求 $f(x) = 0$ 的根就转化成求 $g(x)$ 的不动点的问题。

于是，解决该算法的最大问题就是不动点的存在性与收敛性的判断。

# 不动点的存在性和收敛性

# 不动点的存在性

不动点的存在性是易于描绘的。

设 $f(x)$ 在 $[a,b]$ 内有定义，且在 $(a,b)$ 内可导，则若 $f(x) \in [a,b], \forall x \in [a,b]$. 则 $f(x)$ 在 $[a,b]$ 内存在不动点。

该定理根据介值定理易证，实际上，该定理是压缩映射定理在一维空间上的的特殊形式。同时注意到，$f(x) \in [a,b], \forall x \in [a,b]$ 的条件不是十分苛刻的，甚至是不动点存在所必须的。

# 不动点的收敛性

如果在区间$[a,b]$ 上存在两个或以上的不动点，那么极有可能存在不收敛到欲求的不动点的情况。于是，如果在某些条件下，可以限制在区间$[a,b]$ 内存在唯一的不动点，那么不动点在经过迭代后有更大的概率会收敛。实际上，根据压缩映射定理即可解决这一问题。

# Banach 不动点定理

令 $(X,d)$ 是一个完备的度量空间，若存在映射 $T: X \to X$ 及 $L \in [0,1)$ 使得

$$d(T(x), T(y)) \leq Ld(x,y),$$

则存在唯一的不动点 $x^\star \in X$ 使得 $T(x^\star) = x^\star$, 于是 $\forall x_0 \in X$, 有

$$\lim_{n \to \infty}T^{(n)}(x_0) = x^\star,$$

即任取一点进行迭代都是收敛的。该定理称为 Banach 不动点定理 (Banach fixed point theorem), 又称压缩映射定理 (contraction mapping theorem). 其中的映射 $T$ 称为压缩映射 (contraction mapping).

证明是容易的。

唯一不动点可以采用反证法证明。若$\exists x_1^\star, x_2^\star$ 都为不动点，则$d(x_1^\star, x_2^\star) = d(T(x_1^\star),T( x_2^\star)) \leq qd(x_1^\star, x_2^\star)$, 矛盾。

迭代收敛根据压缩映射的性质即可证明。$\forall x_0 \in X$, $d(T^{(n)}(x_0), T^{(n)}(x^\star)) \leq q^nd(x_0, x^\star)$, 于是$n\to \infty$, 有$d(T^{(n)}(x_0),T^{(n)}(x^\star)) \to 0$, 即证。

# 不动点迭代的求解

不动点迭代的算法十分简单，仅包含一个迭代。算法代码如下：

//input: equation f(x)=x, initial approximation x0, tolerance TOL, maximum number of iterations N

//output: approximate solution x or message of failure

for (int i=1; i<=N; i++){

    double x = f(x0);

    if (-TOL < x-x0 && x-x0 < TOL) return x;

    x0 = x;

}

# 收敛速度分析

不动点迭代法的收敛速度$\displaystyle \lim_{n \to \infty}\frac{x_{n+1} - x^\star}{x_{n} - x^\star} = \lim_{n \to \infty}\frac{f(x_n) - x^\star}{x_n - x^\star} \leq L$, 于是在李普希茨常数$L$ 估计恰当的情况下，不动点迭代是线性收敛的，且渐近误差常数为李普希茨常数$L$.

# 牛顿法

# 基本想法

牛顿法 (Newton method) 同样是基于迭代的算法。其想法基于泰勒展开或几何估计。

若$f(p)=0$, 则对$f(x)$ 在$x=p_0$ 处泰勒展开，得到

$$f(p) = f(p_0) + (p-p_0)f'(p_0) + \frac{(p-p_0)^2}{2}f''(\xi(p))$$

近似地，有

$$0\approx f(p_0) + (p-p_0)f'(p_0)$$

于是可以对$p$ 作估计：

$$p\approx p_0 - \frac{f(p_0)}{f'(p_0)}$$

这就是牛顿法的基本想法。

# 算法

牛顿法在算法中不断迭代$p$ 以取得更高的精度。其算法如下：

//input: function f(x), initial approximation p0, tolerance TOL, maximum number of iterations N

//output: approximate solution p or message of failure

for (int i=1; i<=N; i++) {

    double p = p0 - f(p0)/df(p0); //df(x) means the derivative function of f

    if (-TOL <= p-p0 && p-p0 <= TOL) return p;

    p0 = p;

}

像二分法一样，我们也可以选择不同的停机方式。

# 牛顿法的收敛性

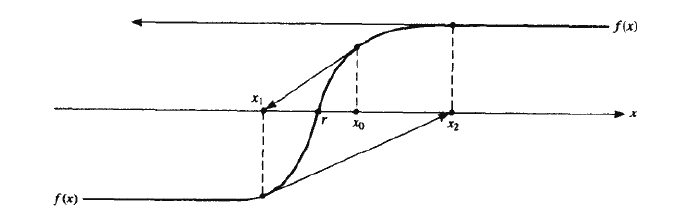
牛顿法并不是时刻收敛的，事实上，只有选取的初值$p_0$ 充分接近$p$, 才能保证迭代产生的序列$\{p_n\}_{n=0}^\infty$ 收敛。下图是一个牛顿法不收敛的例子。

# 牛顿法的改进

# 正割法

在牛顿法中，为解决求导困难的问题，采用

$$f'(p_{n-1}) \approx \frac{f(p_{n-1}) - f(p_{n-2})}{p_{n-1} - p_{n-2}}$$

估计，

该方法的收敛速度慢于牛顿法，但因为简化了导数的计算，最终的计算速度一般快于牛顿法 (与具体函数有关)。

其算法如下：

//input: function f(x), initial approximations p0, p1, tolerance TOL, maximum number of iterations N

//output: approximate solution p or message of failure

double q0 = f(p0);

double q1 = f(p1);

for (int i=2; i<=N; i++) {

    double p = p1 - q1*(p1 - p0)/(q1 - q0);

    if (-TOL <= p-p1 && p-p1 <= TOL) return p;

    p0 = p1;

    q0 = q1;

    p1 = p;

    q1 = f(p);

}