# 计算机图形学概述

# 概念

# 图形学的目的

The screen is a window through which one sees a virtual world. The challenge is to make that world look real, act real, sound real, feel real.
Sutherland 1965

# 图形学的概念

Computer graphics are pictures and films created using computers. Usually, the term refers to computer-generated image data. It focuses on the mathematical and computational foundations of image generation and processing.
Wikipedia

# 图形学的应用

计算机图形学的一些应用包括

娱乐和艺术
- 游戏制作 (Games)
- 电影制作 (Movies)
- 非真实感渲染 (Non-Photographic Rendering, NPR)
计算机辅助设计 (Computer Aided Design, CAD) 和制造 (Manufacturing, CAM)
图形用户界面 (Graphical User Interface, GUI)
可视化 (Visualization)
医学成像 (Medical Imaging)
机器人学 (Robotics)

# 计算机图形学课程

在计算机图形学课程上，需要学习的重点内容如下：

模型及视点变换 (Modeling & View Transformations)
图形学管线 (Graphics Pipeline)
动画 (Animation) 和色彩 (Color)
光线投射 (Ray Casting) 和光线追踪 (Ray Tracing)
纹理 (Textures) 和阴影 (Shadows)
采样 (Sampling) 和全局光照 (Global Illumination)
算法实现 (Implementation Algorithms)

# 图形学学术会议及刊物

图形学中的主要学术刊物和会议包括

SIGGRAPH
SIGGRAPH ASIA
Euro Graphics (EG)
Pacific Graphics (PG)
Symposium of Physical Modeling
Symposium of Geometric Modeling
China Graph
CAD/Graphics

# 渲染管线

将图形学的渲染过程流水线化，可以得到图形学的渲染管线 (pipeline).

顶点处理 (vertex processing): 实现顶点坐标在不同坐标系中的转换
图元组装 (primitive Assembly): 图元组装过程将顶点按某些规则进行组合，得到线段、多边形、多面体等多种图元
裁剪 (clipping): 裁剪过程提取虚拟摄像机中可以看到的图元
光栅化 (rasterization): 将图元转换为片元，即一系列具有色彩和深度信息的点组成的片
片元处理 (fragment processing):

# OpenGL 基础

# 一个最简单的 OpenGL 程序

main.c

	#include <GL/glut.h>
	int main(int argc, char** argv)
	{
	glutInit(&argc,argv);
	glutInitDisplayMode(GLUT_SINGLE\|GLUT_RGB);
	glutInitWindowSize(500,500);
	glutInitWindowPosition(0,0);
	glutCreateWindow("simple");
	glutDisplayFunc(mydisplay);
	init();
	glutMainLoop():
	}

	void init()
	{
	glClearColor(0.0, 0.0, 0.0, 1.0); // 指定背景色
	glColor3f(1.0, 1.0, 1.0);
	glMatrixMode (GL_PROJECTION); // 确定变换形式
	glLoadIdentity ();
	glOrtho(-1.0, 1.0, -1.0, 1.0, -1.0, 1.0); // 设置可见范围
	}

	void mydisplay()
	{
	glClear(GL_COLOR_BUFFER_BIT);
	glBegin(GL_POLYGON);
	glVertex2f(-0.5, -0.5);
	glVertex2f(-0.5, 0.5);
	glVertex2f(0.5, 0.5);
	glVertex2f(0.5, -0.5);
	glEnd();
	glFlush(); // 强制刷新缓冲，以执行绘制命令
	}

# GLUT 函数

glutInit : allows application to get command line arguments and initializes system
gluInitDisplayMode requests properties for the window (the rendering context)
- RGB color
- Single buffering
- Properties logically ORed together
glutWindowSize in pixels
glutWindowPosition from top-left corner of display
glutCreateWindow create window with title “simple”
glutDisplayFunc display callback
glutMainLoop enter infinite event loop

#

glVertex2fv(GLfloat *a) : 画一个坐标为 a 的顶点
glMatrixMode :

# color

glShadeModel() : 设置着色模式，选项包括
- GL_SMOOTH : 光滑着色，即多边形内部颜色进行插值
- GL_FLAT : 恒定着色

# 几何与变换

几何研究的是空间中的元素及其关系。计算机图形学研究的是三维空间中的几何。其中的几何元素主要包括点和向量。在图形学中，由于需要关注位置信息，一般认为平移后的向量是不相同的。

变换是图形学中几何研究的核心，需要学习的重点是变换的数学表示和内在意义。

# 仿射空间

仿射空间 (Affine Space) 是点和向量组成的空间。其中定义的基本运算包括向量和、标量 - 向量积、点 - 向量和和标量运算。

# 变换

基本的变换包括旋转 (Rotation)、缩放 (Scaling)、反射 (Reflection)、平移 (Translation)、剪切 (Shearing) 等。

按照不同的标准，以上的变换可以进行简单的归类。

刚体变换 (Rigid-Body Transformation), 又称欧式变换 (Euclidean Transformation), 包括旋转和平移变换。此类变换保持距离和角度。

相似变换 (Similarity Transformation), 包括刚体变换和各向同的缩放变换 (Isotropic Scaling). 此类变换保持角度。

线性变换 (Linear Transformation), 包括除平移外的全部相似变换，以及一般的缩放变换、反射和剪切变换。

注意到，平移变换不保持线性。假设某平移变换为 $f$ , 则显然 $\alpha f(v) \neq f(\alpha v)$ . 这也是引入齐次坐标的主要原因。

仿射变换 (Affine Transformation), 包括以上所有变换。其特点是可以保持平行性，即平行的两直线仿射变换后依然平行。

射影变换 (Projective Transformation), 在仿射变换的基础上引入射影变换，此时能保持线性和比例，即直线在射影变换后依然是直线，且定比分点变换前后比例不变。

# 齐次坐标

表示仿射空间中元素的一个方式是借助齐次坐标 (homogeneous coordinate). 在 $d$ 维空间中，一个点的坐标表示为 $(x_1,x_2,\dots,x_d,1)$ , 一个向量的坐标表示为 $(v_1,v_2, \dots, v_n, 0)$ . 这样，可以采用通常的向量计算统一仿射空间中的基本运算。下面，我们一般认为我们讨论的是三维空间的其次坐标，即齐次坐标共 $4$ 个分量。

# 记号表示

在仿射空间中，我们习惯的记号表示如下：

大写字母 ( $P,Q,R$ ): 表示仿射空间中的点
小写字母 ( $u,v,w$ ): 表示仿射空间中的向量
小写希腊字母 ( $\alpha, \beta, \gamma$ ): 表示标量
粗体字母 ( $\boldsymbol{p}, \boldsymbol{q}, \boldsymbol{u}, \boldsymbol{v}$ ): 表示点和向量的变换，实际上是一个由 $4$ 个标量组成的齐次坐标

# 齐次坐标的几何意义与扩展

注意到，一个 $d$ 维空间中的齐次坐标为 $(d+1)$ 维度，因此可以看作 $(d+1)$ 维空间中的一个点或向量。以二维空间为例，此时，点 $X(x,y,1)$ 可以看作一条射线 $(tx,ty,t),\, t\in \mathbb{R}$ 与平面 $z=1$ 的交点。而所有的向量与 $z=1$ 平行，因此点与向量的和仍在 $z=1$ 平面内。

在此种意义下，我们可以采用直线 $(tx,ty,t), \, t\in \mathbb{R}$ 表示一个点，因此点的最后一维坐标不再限制为 $1$ .

# 坐标系变换

在齐次坐标系统中，坐标系的变换方式仍然适用。

假设两坐标系中基向量分别为 $(u_1,u_2,u_3)$ 及 $(v_1,v_2,v_3)$ , 坐标原点依次为 $P_0,\, Q_0$ . 其中 $v_i = \sum_{j=1}^3\gamma_{ij}u_j,\, i=1,2,3$ , 且 $Q_0 = \sum_{j=1}^3\gamma_{4j}v_j + P_0$ .

那么，坐标系变换可以写成一个变换矩阵：

$\left(\begin{matrix} v_1 \\ v_2 \\ v_3 \\ Q_0 \end{matrix}\right) = \left(\begin{matrix} \gamma_{11} & \gamma_{12} & \gamma_{13} & 0\\ \gamma_{21} & \gamma_{22} & \gamma_{23} & 0\\ \gamma_{31} & \gamma_{32} & \gamma_{33} & 0\\ \gamma_{41} & \gamma_{42} & \gamma_{43} & 1\\ \end{matrix}\right) \left(\begin{matrix} u_1 \\ u_2 \\ u_3 \\ P_0 \end{matrix}\right)$

显然，矩阵 $M=(\gamma_{ij})$ 是可逆矩阵。且其逆表示从 $(v_1,v_2,v_3)$ 到 $(u_1,u_2,u_3)$ 的坐标变换。

注意到，坐标系变换是全体仿射变换的总和。因此，可以采用形如

$\left(\begin{matrix} \gamma_{11} & \gamma_{12} & \gamma_{13} & 0\\ \gamma_{21} & \gamma_{22} & \gamma_{23} & 0\\ \gamma_{31} & \gamma_{32} & \gamma_{33} & 0\\ \gamma_{41} & \gamma_{42} & \gamma_{43} & 1\\ \end{matrix}\right)$

的矩阵表示齐次坐标下三维物体的全体仿射变换。

下面，我们给出前述基本变换的矩阵形式。

# 平移变换

点 $P(x,y,z,1)$ 经平移变换 $\boldsymbol{d}(d_x,d_y,d_z,0)$ 到达 $P'(x',y',z',1)$ , 则变换矩阵为

$\left(\begin{matrix} x' \\ y' \\ z' \\ 1 \end{matrix}\right) = \left(\begin{matrix} 1 & 0 & 0 & d_x \\ 0 & 1 & 0 & d_y \\ 0 & 0 & 1 & d_z \\ 0 & 0 & 0 & 1 \end{matrix}\right) \left(\begin{matrix} x \\ y \\ z \\ 1 \end{matrix}\right)$

# 旋转变换

在三维空间下，绕 $z$ 轴的旋转变换矩阵可以表示为

$\bm{R}_z(\theta) = \left(\begin{matrix} \cos \theta & -\sin \theta & 0 & 0\\ \sin \theta & \cos \theta & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{matrix}\right)$

类似地，绕 $x$ 轴的旋转变换矩阵可以表示为

$\bm{R}_x(\theta) = \left(\begin{matrix} 1 & 0 & 0 & 0\\ 0 & \cos \theta & -\sin \theta& 0\\ 0 & \sin \theta & \cos \theta& 0\\ 0 & 0 & 0 & 1 \end{matrix}\right)$

绕 $y$ 的旋转变换矩阵可以表示为

$\bm{R}_x(\theta) = \left(\begin{matrix} \cos \theta & 0 & \sin \theta & 0\\ 0 & 1 & 0 & 0\\ -\sin \theta & 0 & \cos \theta& 0\\ 0 & 0 & 0 & 1 \end{matrix}\right)$

# 缩放变换和反射变换

缩放变换矩阵可以表示为

$\bm{S}(s_x,s_y,s_z) = \left(\begin{matrix} s_x & 0 & 0 & 0 \\ 0 & s_y & 0 & 0 \\ 0 & 0 & s_z & 0 \\ 0 & 0 & 0 & 1 \\ \end{matrix}\right)$

反射变换可以看作特殊的缩放变换，只需要令某 $s_i = -1$ 即可。

# 变换的复合关系

注意到，矩阵乘法具有结合律，因此变换的复合满足结合律。但上述大多矩阵相乘是不可交换的，因此变换复合一般不满足交换律。

# OpenGL 中的变换表示

# 矩阵模式

OpenGL 中的

名称	功能
`glLoadIdentity()`	加载模型建筑法

# 四元数

四元数 (quaternion) 的一般代数形式为 $q=a+bi+cj+dk$ , 其中 $a,b,c,d \in \mathbb{R}, \, i^2 = j^2 = k^2 = ijk = -1$ .

基于上述规则，可以定义标量对四元数的乘法及四元数的加法和乘法.

若 $q_1 = a+bi+cj+dkm,\, q_2 = e+fi+gj+hk$ , 则

$q_1+q_2 = (a+e)+(b+f)i+(c+g)j+(d+h)k\\ sq_1 = sa+sbi+scj+sdk\\$

# 3D Viewing

三维观察解决的问题是如何将三维空间中的物体正确投影到二维平面上。包括以下三部分：

Classical Viewing
Computer Viewing
Projection Viewing

# 经典观察 (Classical Viewing)

经典观察 (Classical Viewing) 关注投影现象在数学和艺术中的经典表述方式。

# 观察的基本要素

形成一个有效的观察包括三个基本的要素：

一个或多个被观察的物体 (object), 即观察的对象
观察者 (viewer) 及投影表面 (projection surface), 即观察的载体
从物体传播到投影表面的光线或投影媒介 (projector)

我们观察的物体，都可以也将被离散成一个一个的三角面片并最终实现投影变换。

# 投影的基本分类

平面几何投影可以进行如下分类：

平面几何投影 (planar geometric projections)
- 平行投影 (parallel)
  - 多视图正投影 (multiview orthographic)
  - 轴测投影 (axonometric): 根据坐标轴保持不同比率的数目分类
    - 等测投影 (isometric)
    - 二测投影 (dimetric)
    - 三测投影 (trimetric)
  - 斜投影 (oblique)
- 透视投影 (perspective)
  - 一点透视
  - 两点透视
  - 三点透视

只需要熟知上述透视的作图方式及特点即可。

# 计算机上的观察 (Computer Viewing)

计算机上的观察过程需要考虑如何在计算机中模拟现实世界中的观察。因此，其一般包括三个过程。三个过程的通俗讲法如下：

放置摄像机 (positioning the camera): 即选择恰当的模型矩阵 (model-view matrix). 也就是前面所提及的旋转、平移和缩放等矩阵。
选择镜头 (selecting a lens): 选择恰当的投影矩阵 (projection matrix).
裁剪 (clipping): 即选择恰当的观察视角，对应视角矩阵 (view volume matrix).

是的，这就是 Games101 中所言的 MVP 变换

# 投影矩阵 (Projection Matrix)

观察过程的流水线包括以下步骤

模型和视图变换 (model-view transformation):
投影变换 (projection transformation):
透视分割 (perspective division): 从 4D 到 3D
裁剪 (clipping):
投影 (projection): 从 3D 到 2D

# 光线追踪

# 着色 (Shading)

着色 (shading) 是根据材质属性和光源，计算沿着视线的出射光亮度的过程。我们使用的着色方程具有漫反射和镜面反射分量。其包括光照 (illumination) 计算和明暗处理两个部分，但常常混为一谈。

在考虑物体的明暗处理时，需要考虑的内容知识包括：

光源 (light source)
- 光照模型包括两类：局部光照 (local lighting) 和全局光照 (global lighting)。相对于局部光照，全局光站考虑了来自其余物体的反射光，而不是仅考虑光源。
材质 (material properties)
- 不同材质的透光率和吸收率不同，导致其在相同光照下的效果不同。
观察者位置 (location of viewer)
- 采用能量守恒的办法，计算困难
物理表面朝向 (surface orientation)

# 自然界中的光照特点

在进行光照模拟之前，需要先对自然界中的光照特点进行抽象和归纳。

当光照射到物体表面后，可能发生反射、折射和吸收.

# 光的辐射度量

辐射能通量或辐射功率定义为单位时间内光源发出或一定截面接收的辐射能，记作 $\Psi$ , 单位是瓦 ( $W$ ). 光的辐射能通量可以按照波长分解，即

$\Psi = \int\psi(\lambda) \mathrm{d}\lambda$

其中 $\psi(\lambda)$ 称为辐射能通量的谱密度。

# 发光强度和亮度

点光源 $Q$ 沿某一方向 $\boldsymbol{r}$ 的发光强度 $I$ 定义为其沿此方向上单位立体角发出的光通量。即

$I = \frac{\mathrm d\Psi}{\mathrm d\Omega}$

这样，我们可以定义面元 $\mathrm dS$ 在 $\boldsymbol{r}$ 上的光度学亮度 (简称亮度) 为

$B = \frac{\mathrm dI}{\mathrm dS^*} = \frac{\mathrm dI}{\mathrm dS\cos \theta}$

其中 $\mathrm dS^*$ 表示面元的投影面积， $\theta$ 是面元和投影面的夹角。

# 局部光照模型

在上述物理学背景的基础上，我们可以得到光照简单描述方式，即局部光照模型。其特点是，

明暗处理的 Phong 模型

# Shading 中的 OpenGL API

不采用 GLColor 进行物体绘制。

# 光线追踪

# 裁剪 (Clipping)

裁剪 (clipping) 是计算机图形学中确定渲染对象和渲染范围的方式。一般情况下，裁剪范围是一个平行于坐标轴的矩形 (2 维) 或长方体 (3 维)。在实现上，关于线段、多边形的裁剪易于实现，但对于曲线、文本的裁剪难以计算。因此，需要将其转化为线段和多面体的裁剪。在原理上，需要考虑基本图元的裁剪，即点、线段和多边形的裁剪。

# 点裁剪

点裁剪只需比较大小即可。当且仅当 $x_{\min} \leq x \leq x_{\max}$ 且 $y_{\min} \leq y \leq y_{\max}$ 时，保留该点，否则去掉该点。

# 线裁剪

线段裁剪的暴力方法是直接计算该线段与矩形各直线的交点，然后进行判断。其缺点是需要计算交点的次数过多，极大影响了渲染效率。因此，对该算法的改进集中于减小交点的计算次数上。

# Cohen-Sutherland 算法

Cohen-Sutherland 算法 (简称 CS 算法) 是线段裁剪的一个朴素优化算法。其想法是，将线段两端点的坐标 $(x_1,y_1),\,(x_2,y_2)$ 与矩形的最大 / 最小坐标 $x_{\min},\,x_{\max},\,y_{\min},\,y_{\max}$ 依次比较，这样可以剔除线段在 $x=x_{\min}$ 左 (等四种对称情况)，以及线段在矩形内部的情况。对于其余的情况，仍需要进行计算。

# Outcode 改进

Cohen-Sutherland 算法中，采用比较方法减少了交点计算。 Outcode 则是对上述算法中比较部分的进一步优化。其将二维图像上的点按裁剪区域进行分类，然后对各区域进行位编码 (如下图)。这样可以将比较运算转化成位运算，从而进一步加速比较。

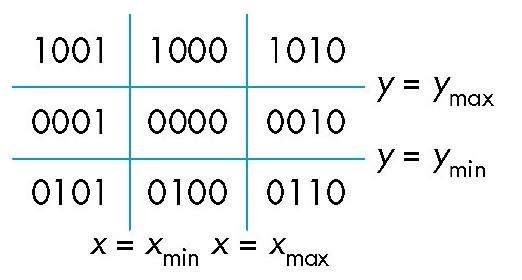
outcode

根据编码规则可以看出，只需要将线段两端点的位编码作异或，若某位值为 $1$ , 则需要计算与该边的交点。

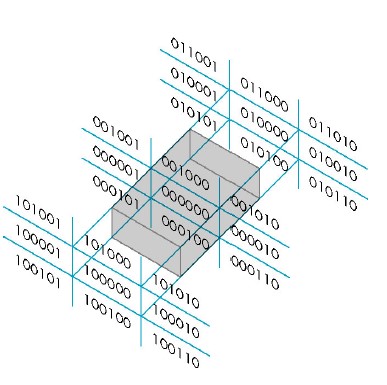
# 3 维 Cohen-Sutherland 算法

只需要将位编码改成 6 位即可推广。

Cohen-Sutherland Algorithm in 3D

# Cyrus-Beck 算法

Cyrus-Beck 算法是将线段采用参数方程表示，计算其与多边形各个边的交点，然后根据参数 $t$ 的大小判断交点。

假设线段为 $P_0P_1$ , 其参数方程为 $P(t) = tP_0 + (1-t)P_1$ , 又在窗口边界 $E$ 上任取一点 $A$ , 假设该边界的外法向量为 $\boldsymbol{n}$ , 则若 $P(t)$ 为交点，根据 $\boldsymbol{n} \cdot (P(t)-A) = 0$ , 代入 $P(t)$ 的表达式得到：

$t = \frac{\boldsymbol{n} \cdot AP_0}{\boldsymbol{n} \cdot P_1P_0}$

此处需要注意表达式的符号

根据参数大小判断交点需要考虑实际情况，即对于线段、射线和直线具有不同区分。若 $t<0$ , 则交点在 $P_0$ 外侧，若 $t>1$ , 则交点在 $P_1$ 外侧，否则 $t \in (0,1)$ , 此时交点在线段 $P_0P_1$ 上。

# 梁友栋 - Barsky 算法

梁友栋 - Barsky 算法是在 Cyrus-Beck 算法上对矩形窗口优化得到的。其参数 $t$ 计算中向量点乘可以用特定坐标的差代替。对于二维矩形，其计算方式如下：

边 $E_i$	外法向量 $\boldsymbol{n}_i$	边上一点 $A$	$AP_0$	$\boldsymbol{n} \cdot AP_0$	$$
上边界 $y=y_T$	$(0,1)$	$(x,y_T)$

参考: 董兰芳：二维观察

# 多边形裁剪算法

多边形裁剪算法 (Clipping Algorithms for Polygons) 主要包括两种：

Sutherland-Hodgman 算法
Weiler-Atherton 算法

# Sutherland-Hodgman 算法

Sutherland-Hodgman 算法最基础的多边形裁剪算法，又称逐边裁剪算法。由于算法设计借助了凸多边形的相交的性质，因此该算法仅适用于凸多边形。算法的主要步骤即对渲染框各边按顺时针顺序依次裁剪，如下图所示：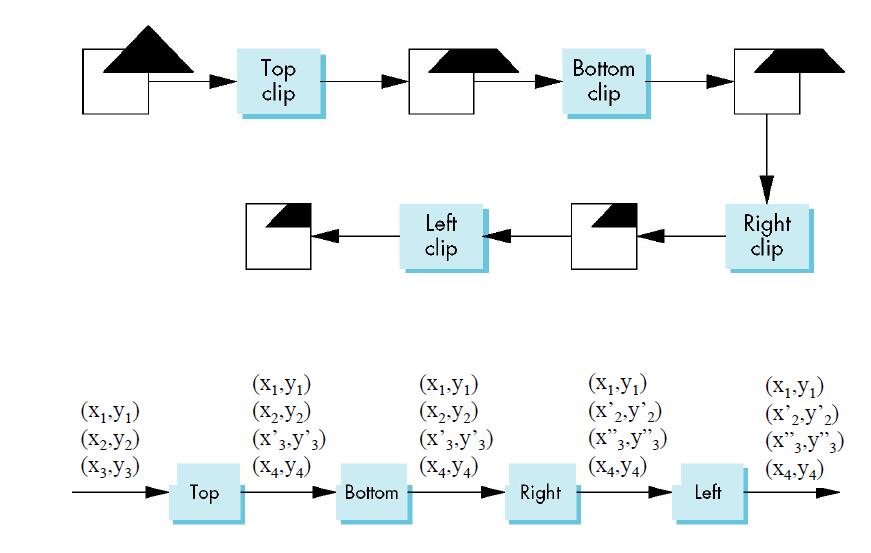

需要注意的是，Sutherland-Hodgman 算法中，每一次裁剪只记录被裁剪图像与渲染框的首末两个交点，将两者连线作为交线。

# Weiler-Atherton 算法

该算法可以适用于凹多边形。算法步骤如下：

从多边形的任一顶点出发，按顺时针寻找一条与裁剪框相交的边。
如果边进入裁剪框，就记录交点。
如果边离开裁剪框，就记录交点，同时在其后将裁剪框视作多边形，多边形视作裁剪框。
最终连接所有视作多边形的边。

# 包围盒算法：多边形裁剪加速

在以上两种算法的基础上，可以采用包围盒进行多边形裁剪的加速。

# 图形学前沿论文阅读 - Fast Forward

# Modeling

# Point2Mesh: A Self-Prior for Deformable Meshes

SIGGRAPH 2020

将点云表达的物体转化为三角形表达。

Self-Prior: 自先验。

# Restricted Delaunay Triangulation for Explicit Surface Reconstruction

水密模型

初始模型和最终模型的拓扑结构不需一致。

# Free2CAD: parsing freehand drawings into CAD commands

根据手绘图像建立对应的 CAD 模型，且模型可以进行交互式修改。

# Symmetry-driven 3D Reconstruction from Concept Sketches

采用基于对称性结构的方法从设计草图进行模型重建。

# Neural 3D Reconstruction in the Wild

借助图像组合生成对应物体的三维模型。

# SPAGHETTI: Editing Implicit Shapes Through Part Aware Generation

disentangle: 解耦

将物体解耦成不同的部件。

# Generation

# GET3D: A Generative Model of High Quality 3D Textured Shapes Learned from Images

从图片生成高质量的三维模型。

# GRAINS: Generative Recursive Autoencoders for INdoor Scenes

室内场景的生成。

# WallPlan: synthesizing floorplans by learning to generate wall graphs

给定图形和约束，生成房间布局。

# Language-driven synthesis of 3D scenes from scene databases

# DreamFusion: Text-to-3D using 2D Diffusion

# Make-A-Video: Text-to-Video Generation without Text-Video Data

只要是内容生成的都属于 Graphics. 不一定是三维模型，也可以是二维图像。

# Rendering

# Unbiased Caustics Rendering Guided by Representative

# NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis

只能渲染相机图片，即现有的图片。而不能渲染虚拟的、计算机产生的图像。

NeRF：用深度学习完成 3D 渲染任务的蹿红 - Leviosa 的文章 - 知乎

研究方向：在稀疏采样下获取真实感

# NeuS: Learning Neural Implicit Surfaces by Volume Rendering for Multi-View R

# NeuTex

# Scalable neural indoor scene rendering

# Neural Rendering in a Room: A model 3D Understanding and Free-Viewpoint Rendering for the Closed Scene Composed of Pre-Captured Objects

提出了新的重要的方向。

# Human modeling

# NeuroSkinning: Automatic Skin Binding for Production Characters with Deep Graph Networks

浙大和网易的合作项目。SIGGRAPH 2019 衣服的模拟

# Dynamic Hair Modeling from Monocular Videos using Deep Neural Networks

采用方向场描述头发的运动。

# Interaction

# Automatic Translation of Music-to-Dance for In-Game Characters

基于音乐生成舞蹈姿势动画。

学点新东西：

半监督学习
自监督学习
对偶四元数
- 对偶数及公式推导
- 对偶四元数，必掌握的 3d 数学神器

# Learning to Use Chopsticks in Diverse Gripping Styles

该文章旨在让机器人学习如何以不同的姿势使用筷子。

逆向动力学 (inverse kinematics, IK): 通过输入动作姿势，解得对应关节的角度大小。是正向运动学输入与输出相反的结果。

参考:Wiki:Inverse kinematics

# Scene mover: automatic move planning for scene arrangement by deep reinforcement learning

采用蒙特卡洛树进行搜索，从而解决二维移动布局问题。

# Deep Network for Geometric Processing

# Subdivision-Based Mesh Convolution Networks

要求：

写明作者及单位
该讲哪些东西：
1. 做了什么事情 --question
2. 比别人好在哪里 -- 创新点
3. 怎么证明其好于别人 --experiment
4. 借鉴的经典方法 --Reference

https://www.pbr-book.org/3ed-2018/contents