这是关于论文 Group Equivariant Convolutional Networks 的笔记。

# Background

该文章是 Cohen 与 Max Welling 于 ICML 2016 上发表的一篇文章。

在当时，学界已经认可卷积网络在图像识别上的重要性。但图像进行旋转、翻转等简单操作后，卷积网络却难以识别对应的内容。对于发生平移的内容，卷积网络却可以识别。

在当时，一般采用数据增强方法解决该问题，即将旋转不同角度的图像、翻转的图像都作为训练集放入网络中。但这一行为属于头痛医头脚痛医脚，仅仅在表面上解决了问题。

这篇文章从这样一个问题出发，将群论融合进入卷积网络的对称性（归纳偏置），发现了卷积核在平移变换中的等变性 (equivariant), 并进一步提出了群等变卷积网络。

# 壁纸群

在介绍等变性之前，我们先来简单了解一下壁纸群 (wallpaper group). 壁纸群并不是 Wallpaper Engine 的图片交流群，而是一系列平面对称群，共 17 种。

壁纸群用来描述某一个单位图像如何通过基本变换得到密铺整个墙面的墙纸。在高中化学中，我们研究了空间中的密铺最小子单元 —— 晶胞，它的形状为平行六面体。在此处，壁纸群的晶格类型包括平行四边形、菱形、矩形、正方形和六边形。

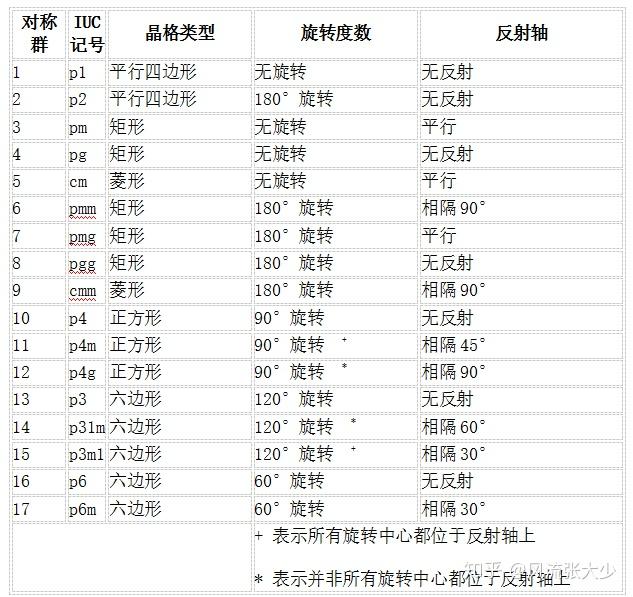
所有的壁纸群类型_图片来源见水印

文中提到的 $p4$ , 是一个小正方形通过绕顶点旋转 $90\degree$ 四次形成一个大正方形，然后平移密铺得到的壁纸。此外，文中还提到了 $p4m$ , 则是通过一个等腰直角三角形对称及旋转共 $8$ 次组成的正方形晶胞平移密铺得到壁纸。

比较直观的展示图还可以看：新坑不填 —— 平面对称群 Wallpaper group - 聂渲南的文章 - 知乎。