在看 CS224W 的 DeepWalk 算法时，发现它实际上是将 word2vec 的算法应用到了图上，因此打算看看 word2vec.

论文地址：Distributed Representations of Words and Phrases and their Compositionality

本文是 NIPS 2013 的最佳论文，也是 word2vec 的原始论文。最近，该论文也刚刚荣获 NIPS 时间检验奖。

此外，我还看了 Efficient Estimation of Word Representations in Vector Space. 这篇文章是上一篇的前身，提出了 CBOW 和 skip-gram 两种模型。

实际上，这同时也是 CS224N-2023Winter 课程中 word2vec 部分的一个简单笔记。

# 词义表示

词语的含义 (meaning) 可以是词语在现实生活中的物象指代，这称之为 denotional idea. 在计算机系统中，我们通常采用分类学 (taxonomy) 的方法表示词语的含义，一个重要的例子是数据集 WordNet.

然而，采用分类法进行词义表述有诸多缺点：

1. 分类法的描述是主观的，即分类法需要人为给出词语的所在类别
2. 分类法难以区分近义词之间的细微差别

实际上，除了上世纪 80 年代关于神经网络的研究和如今的深度学习方法之外，其它关于 NLP 的研究都是将单词进行符号化描述的，一个具体表现是采用 one-hot 编码。这样的表述方法带来的问题就是它忽略了词语之间的内在联系。例如，notebook 和 laptop 本身词汇含义相似，但在 one-hot 编码下，它们天然不具有内在相似性 (inherent similarity), 即两者的余弦相似度是 $0$. 这样的问题不止出现在 NLP 领域的词语表示。事实上，在所有基于概率的传统机器学习领域中，对象之间内在关系被忽略的问题都存在。此处的一个解决方法是建立词语之间的相似性关系。

# 分布相似性

分布相似性 (distributional similarity) 是指，表示某个词汇含义的值只需要从词汇所在的上下文中获取。

You shall know a world by the company it keeps.

by J. R. Firth

维特根斯坦在《哲学研究》中也提到，理解词汇含义的正确方法是从文本中理解。

# 基于前馈神经网络的语言模型

word2vec 之前的语言模型是基于前馈神经网络的语言模型 (Feedforward Neural Network Language Model, NNLM). 其想法是，第 $N+1$ 个词的概率是依赖于前 $N$ 个词的。

这个模型包括四层：

• 输入层：包括 $N$ 个单词的输入，每个单词采用 $V$ 维度的 one-hot 编码。$N$ 的通常取值为 $10$.
• 投影层：将输入投影为 $N \times D$ 的投影层 $P$. 通常情况下 $D \in [500, 2000]$.
• 隐藏层：将输入投影后的每一个 $D$ 维向量转化为一个 $H$ 维向量。通常情况下 $H \in [500, 1000]$.
• 输出层：将隐藏层的每一个 $H$ 维向量转化为一个 $V$ 维度的向量，这个向量表示词汇 $w_i, i = 1, 2, \dots, V$ 的概率分布。

因此，该模型在预测阶段的计算复杂度是

$$Q = N \times D + N \times D \times H + H \times V.$$

在未经优化的模型中，复杂度主导项为 $H \times V$. 但是基于分层 softmax 和二叉树词汇表，我们可以将该项降低为 $H \times \log V$, 此时复杂度的主导项为 $N \times D \times H$.

# word2vec

word2vec 主要包括两种模型：连续词袋模型 (CBOW) 和跳字模型 (skip-gram). 它们都是基于分布相似性的思想。

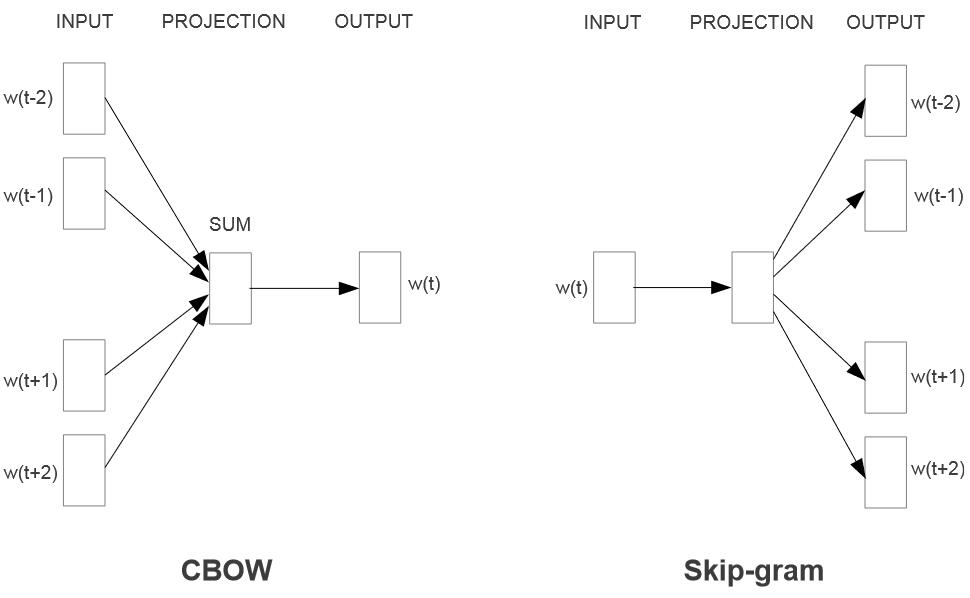
# CBOW

连续词袋模型 (Continuous Bag of Words, CBOW) 的想法是通过连续的多个上下文词汇预测一个词的概率。

CBOW 模型包括下面几个部分：

1. 输入层：CBOW 的输入由上下文词语组成。给定一个固定大小的上下文窗口，模型试图预测在该窗口内缺失的目标词语。假设窗口大小为 2，对于输入序列 "I love natural language processing"，如果目标词是 "natural"，则上下文窗口为 ["I", "love", "language", "processing"]。
2. 嵌入层（Embedding Layer）：每个上下文词语都被映射到一个词向量。这些词向量可以是事先训练好的，也可以是在模型训练过程中学习得到的。这一层的目标是将词语转换为密集的低维向量表示。
3. 汇总层（Summation or Averaging Layer）：CBOW 通过对上下文词向量进行求和或平均来得到一个整体上下文表示。如果是求和，对于上述例子，将得到一个上下文向量："I love language processing"。如果是平均，就是将求和结果除以窗口大小。
4. 输出层：上下文向量通过一个全连接层，输出一个概率分布，表示每个词作为目标词的可能性。通常使用 softmax 函数来进行归一化，得到概率分布。

CBOW 使用梯度下降等优化算法来更新模型参数，以最小化损失函数。在训练过程中，模型通过反向传播算法来调整嵌入层和输出层的权重，以提高对目标词语的预测准确性。

在推理阶段，CBOW 的复杂度是

$$Q = N \times D + D \times \log V.$$

这里词汇表采用 hierarchical softmax 进行优化。

# skip-gram

跳字模型 (skip-gram) 与 CBOW 模型思路相反，其通过中心词预测上下文各词的出现概率。

给定一系列训练单词 $\{w_i | i=1,\dots,T\}$, skip-gram 模型的目的是最大化平均对数概率

$$\frac{1}{T} \sum_{t=1}^T \sum_{-c \leq j \leq c, j \neq 0} \log p(w_{t+j} | w_t),$$

其中 $c$ 是训练窗口大小，$p(w_{t+j}|w_t)$ 的具体定义是基于 Softmax 函数的：

$$p(w_O|w_I) = \frac{\exp(\boldsymbol{v}_O^\top \boldsymbol{v}_I)}{\sum_{w=1}^W \exp(\boldsymbol{v}_w^\top \boldsymbol{v}_I)}$$

skip-gram 模型的各层结构、训练方式与 CBOW 类似。但 skip-gram 模型对于细粒度语义信息即多义词、罕见词的处理效果更好。这是因为 skip-gram 会将包括罕见词在内的每个词都纳入中心词进行概率预测，而 CBOW 则倾向于直接选择出现概率高的词汇。换句话说，两者对权重的加权平均方式不同。

skip-gram 相应的缺点是其训练和推理速度较慢。其推理阶段的计算复杂度为

$$Q = C \times (D + D \times \log V).$$

若窗口长度为 $C$, 则 CBOW 的推理复杂度约为 skip-gram 的推理复杂度的 $1/C$.

# 分层 softmax

分层 Softmax (Hierarchical Softmax) 是一种 softmax 加速近似算法，首先提出于 Hierarchical probabilistic neural network language model. 前面提到，NNLM 等模型在最后阶段的归一化概率时，复杂度受词汇表大小 $V$ 影响。采用层次 Softmax 算法可以加速该项的计算。

分层 Softmax 算法是一个以词频为分类依据的 Huffman 树，将 $V$ 分类问题转化为树高次数的二分类问题，并在二分类上采用 sigmoid 函数模拟 Softmax.

该算法的复杂度为 Huffman 树的查找复杂度也就是 Huffman 编码的平均长度，这是一个接近于信道极限

$$H = - \sum_{i=1}^Vw_i \log_2 w_i$$

的值。基于 Jensen 不等式，有

$$H = - \sum_{i=1}^Vw_i \log_2 w_i \leq -V \cdot \frac{1}{V} \log_2 \frac{1}{V} = \log_2 V.$$

所以采用分层 Softmax 算法后，模型推理的复杂度中 $\mathcal{O}(V)$ 项可以降低到 $\mathcal{O}(\log V)$.

# 负采样

负采样 (negative sampling) 是文章中提出的替代分层 Softmax 的方法。实际上，负采样方法是噪声对比估计的简化和延伸。

# 配分函数

配分函数 (partition function) 是概率分布的归一化因子，即所有概率状态的积分（连续变量）或求和（离散变量），通常用 $Z$ 表示。例如，Softmax 函数中，分母 $\sum_i \exp(\tilde{p}(x_i))$ 就是其配分函数。

如果采用极大似然估计作为目标函数，那么梯度下降可以表示为未归一化概率密度函数的对数与配分函数对数之差：

$$\nabla_{\boldsymbol{\theta}} \log p(\boldsymbol{x}; \boldsymbol{\theta}) = \nabla_{\boldsymbol{\theta}} \log \tilde{p}(\boldsymbol{x}; \boldsymbol{\theta}) - \nabla_{\boldsymbol{\theta}} \log Z(\boldsymbol{\theta}).$$

其中 $\nabla_{\boldsymbol{\theta}} \log \tilde{p}(\boldsymbol{x}; \boldsymbol{\theta})$ 称为正相 (positive phase), 而 $\nabla_{\boldsymbol{\theta}} \log Z(\boldsymbol{\theta})$ 称为负相 (negative phase). 该式称为正相 - 负相分解。

在梯度下降过程中，一般模型的正相可以直接计算得到，而负相则需要整个数据集才能得到结果。于是，人们开始尝试探索负相的估计方法。

分析负相，可以得到

$$\nabla_{\boldsymbol{\theta}} \log Z(\boldsymbol{\theta}) = \frac{\nabla_{\boldsymbol{\theta}}Z}{Z} = \frac{\nabla_{\boldsymbol{\theta}} \sum_i \tilde{p}(x_i)}{Z} = \frac{\sum_i \nabla_{\boldsymbol{\theta}} \tilde{p}(x_i)}{Z}$$

注意到，$\nabla_{\boldsymbol{\theta}} \tilde{p}(\boldsymbol{x}) = \tilde{p}(\boldsymbol{x})\nabla_{\boldsymbol{\theta}} \log \tilde{p}(\boldsymbol{x})$, 于是上式可以转化为

$$\nabla_{\boldsymbol{\theta}} \log Z(\boldsymbol{\theta}) = \frac{\sum_i \tilde{p}(x_i)\nabla_{\boldsymbol{\theta}} \log \tilde{p}(x_i)}{Z} = \sum_i p(x_i)\nabla_{\boldsymbol{\theta}} \log \tilde{p}(x_i) = \mathbb{E}_{\boldsymbol{x} \sim p(\boldsymbol{x})} \nabla_{\boldsymbol{\theta}} \log \tilde{p}(\boldsymbol{x}).$$

我们得到

$$\nabla_{\boldsymbol{\theta}} \log Z(\boldsymbol{\theta}) = \mathbb{E}_{\boldsymbol{x} \sim p(\boldsymbol{x})} \nabla_{\boldsymbol{\theta}} \log \tilde{p}(\boldsymbol{x}).$$

该式左侧是负相（配分函数对数），右侧是未归一化概率分布对数的期望。因此，可以采用 Monte-Calo 采样进行估计。这就是负相估计的理论基础。噪声对比估计和负采样就是在此理论基础上进行的。

# 噪声对比估计

噪声对比估计 (Noise-Contrastive Estimation, NCE) 方法是估计大规模数据配分函数的一种近似方法，在《深度学习》（花书）第 18 章中有较详细的介绍。

# 负采样

将 NCE 的计算形式进行简化得到的。

# Ref

部分内容采用 AI 辅助创作。

• word2vec 常见考点 - frostjsy - CSDN
• Hierarchical Softmax（层次 Softmax） - 夜莺飞鱼 - 知乎
• Noise Constractive Estimation 噪声对比估计 - 我要给主播生猴子的文章 - 知乎
• Noise Contrastive Estimation 前世今生 —— 从 NCE 到 InfoNCE - Apathy 的文章 - 知乎