该实验旨在探究学习率与梯度下降速度及效果的关系。

# Experiment 2: Multivariate Linear Regression

This is the report of Experiment 2: Multivariate Linear Regression.

# Purpose

In this experiment, we want to find the influence of learning rate($\alpha$) on convergence and gradient decent efficiency.

The value of inputs $x^{(i)}$ is the living area and the number of bedrooms, the outputs $y^{(i)}$ are the housing prices in Portland, Oregon.

# Hypothesis

We hypothesize that living area and the number of bedrooms ($\boldsymbol{x}$) are linear independent with housing prices ($y$).

# Procedure

Because I want to figure out the influence of learning rate($\alpha$), I choose different $\alpha$, and draw the change of cost function $J(\theta)$ in $50$ iterations. The cost function $J(\theta)$ is defined as:

$$J(\theta) := \frac{1}{2m}\sum_{i=1}^m\left(h_\theta({x}^{(i)}-{y}^{(i)}\right)^2 = \frac{1}{2m}(X\theta - \vec{y})^\top(X\theta - \vec{y})$$

# Answer of the questions

# Question 5.1

I choose $4$ different $\alpha$ to draw the picture. The results are like these:

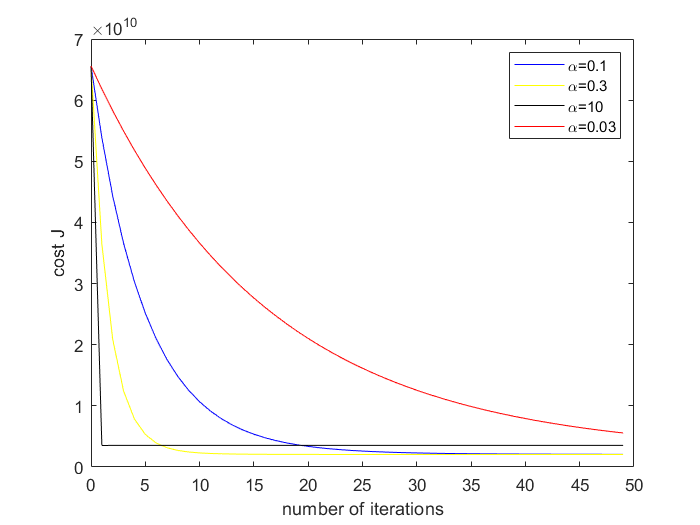
I found that when the learning rate is too small, the convergence speed is too slow. For example, when $\alpha = 0.03$, we can't find the minimum value of $J(\theta)$ after $50$ iterations. When the learning rate is too large, it may be get the optimal $\theta$ in few iterations, but $J(\theta)$ will not converge, but will keep oscillating around the minimum of $J(\theta)$.

# Question 5.2

I choose $\alpha = 0.1$, after $50$ iterations,

$$\theta = (337967.476969,103305.562027,-252.101002)^\top$$

Using that $\theta$, the predicted price of a house with $1650$ square feet and 3 bedrooms is $292437.89$.

# Question 6

With the formula $\theta = (X^\top X)^{-1}X^\top \vec{y}$, I got that

$$\theta = (89597.909543,139.210674,-8738.019112)^\top$$

Using this $\theta$, the predicted price of a house with $1650$ square feet and 3 bedrooms is $293081.46$. The price didn't same, but the error is within the allowable range.