探究正则化系数应对欠拟合、过拟合的效果。

# Experiment 6: Regularization

This is the report of Experiment 6: Regularization.

# Purpose

In this experiment, we want to find the purpose of regularization term on underfitting and overfitting.

The first group of data is a regression problem with single argument. We will try fitting a 5th-order polynomial to a data set of only 7 points.

The second group of data is a classification problem with logistic regression. We also want to find the influence of regularization parameter on underfitting and overfitting.

# Hypothesis

For the first sub-experiment, our hypothesis will be

$$h_\theta(x) = \theta_0 + \sum_{i=1}^5\theta_ix^i$$

For the second sub-experiment, our hypothesis will be

$$h_\theta(x) = g(\theta^\top x) = \frac{1}{1+e^{-\theta^\top x}} = \mathbb{P}(y=1\big|x;\theta)$$

# Procedure

# Regularized Linear Regression

With the hypothesis

$$h_\theta(x) = \theta_0 + \sum_{i=1}^5\theta_ix^i$$

we can get the cost function with respect to $\theta$:

$$J(\theta) = \frac{1}{2m}\left(\sum_{i=1}^m\left(h_{\theta}(x^{(i)})-y^{(i)}\right)^2 + \lambda \sum_{j=1}^n \theta_j^2 \right)$$

where $\lambda$ is the regularization parameter.

Using the normal equations

$$\theta = \left(X^\top X + \lambda \text{diag}\left\{0,1,\dots,1\right\}_{n+1}\right)^{-1}X^\top y$$

When $\lambda = 0, 1, 10$, we got the figure as follows: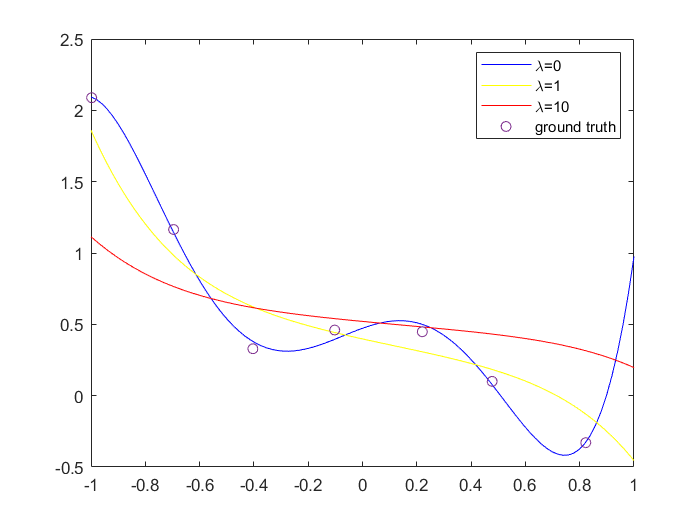

# Regularized Logistic Regression

With the hypothesis

$$h_\theta(x) = g(\theta^\top x) = \frac{1}{1+e^{-\theta^\top x}} = \mathbb{P}(y=1\big|x;\theta)$$

the cost function in regularized logistic regression is

$$J(\theta) = -\frac{1}{m}\sum_{i=1}^m\left(y^{(i)}\log\left(h_{\theta}(x^{(i)}) + (1-y^{(i)})\log\left(1-h_{\theta}(x^{(i)})\right)\right)\right) + \frac{\lambda}{2m}\sum_{j=1}^n\theta_j^2$$

The Newton's Method rule is

$$\theta^{(t+1)} = \theta^{(t)} - H^{-1}\nabla_\theta J$$

With 10 iterations, we get the results as follow:

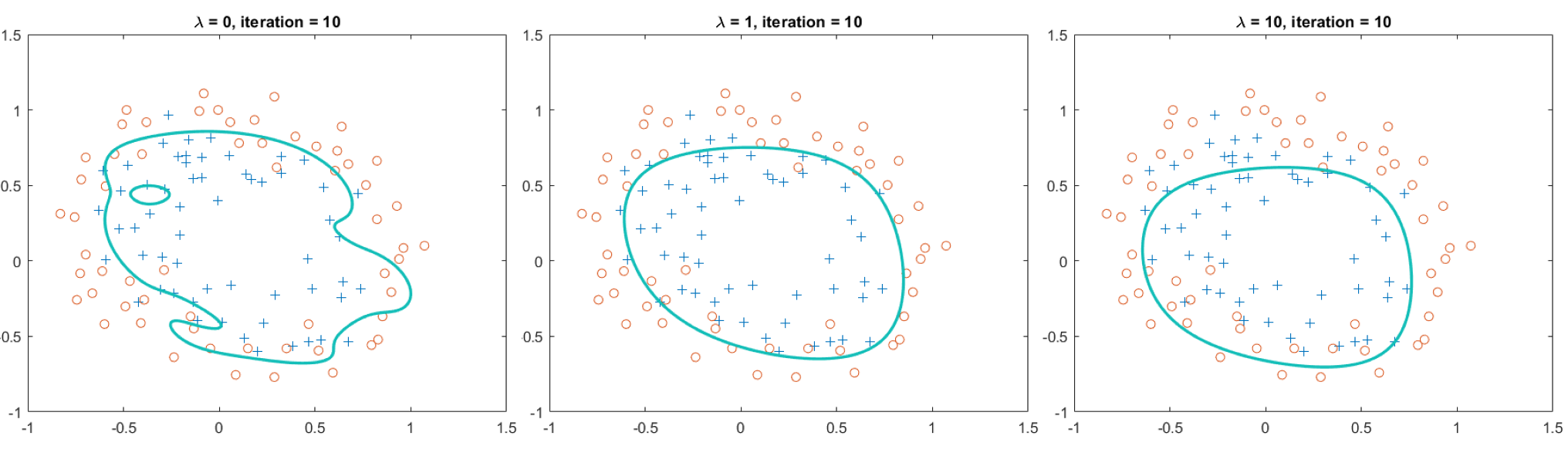
# Answer of the questions

# Question 1

From looking at these graphs(in Exp6-1), what conclusions can you make about how the regularization parameter affects your model?

I found that the larger the $\lambda$, the smoother the curve of the polynomial, which means the polynomial is approximating a line.

# Question 2

How does $\lambda$ affect the results?

Not only $\lambda$ affect the shape of the curve, it also affect the topological structure of the curve. For example, there is a hole when $\lambda = 0$, and the hold disappear while $\lambda = 1$ or $10$.