终于下定决心把之前欠下的东西补上。
# 概述
拓扑的主要性质包括:
- 分离性
- 可数性
- 紧致性
# 分离公理
分离公理 (separation axioms) 是用来描述两个点或者闭集之间能否用邻域分隔的性质,是对拓扑空间的附加要求。在这里用一张 sola 文章 中的图解释:
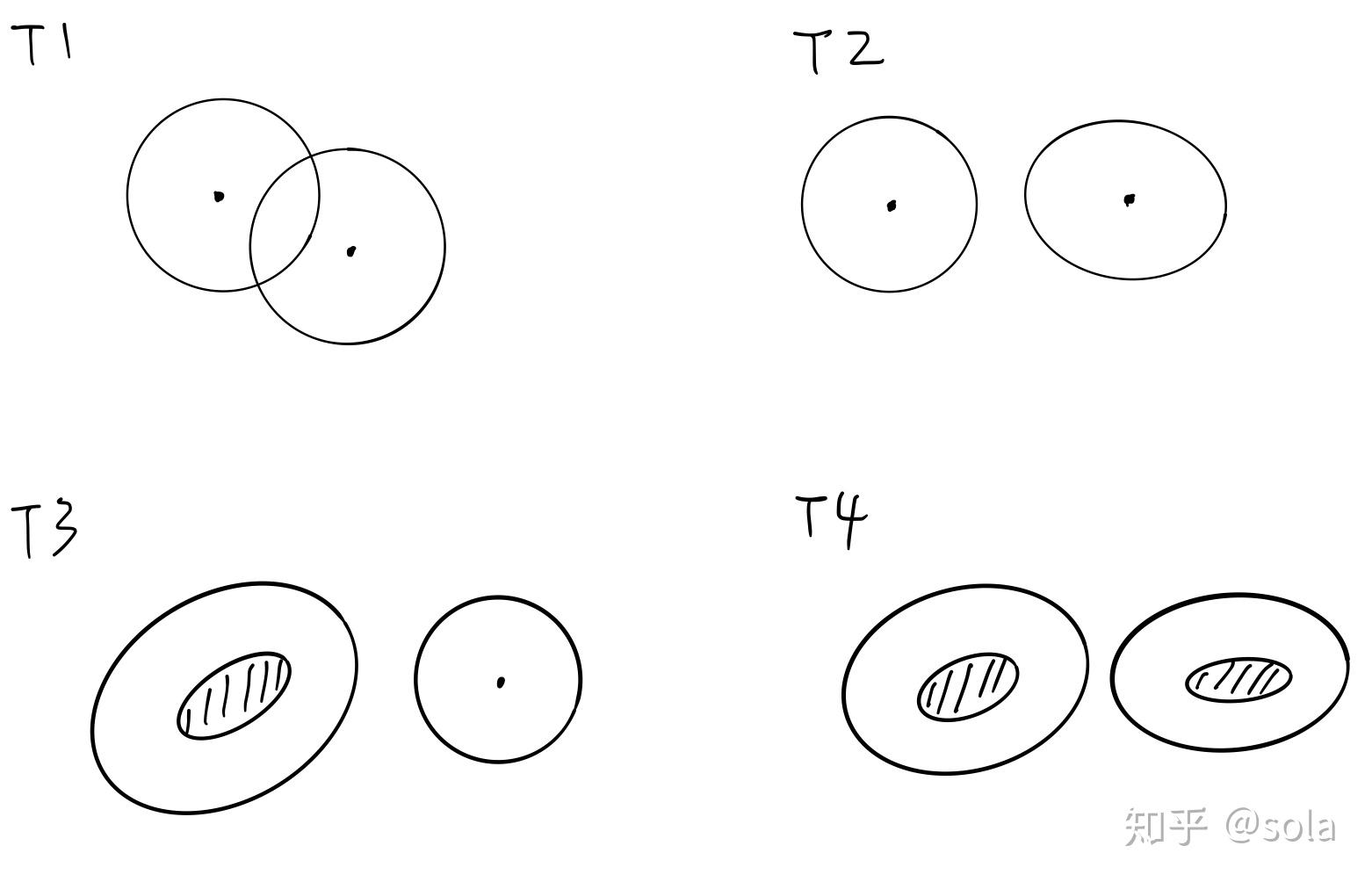
- 公理:任意两个不同点 与 , 有邻域不含 , 有邻域不含 .
- 公理:任何两个不同点有不相交的邻域。
公理是最重要的分离公理,满足该公理的空间称为豪斯多夫空间 (Hausdorff space).
其实其它几个也有名字来着,尽管不太常用。满足 公理的叫弗雷歇空间 (Fréchet space), 满足 公理的叫正则豪斯多夫空间 (regular Hausdorff space), 满足 公理的叫正规豪斯多夫空间 (normal Hausdorff space).
注意实数集上的余有限拓扑 , 对于点 , 其存在邻域 不含 . 类似,点 也存在邻域 不含 , 因此其满足 公理。但由于该拓扑是 “余有限” 的,因此任意两邻域必定相交,因此不满足 公理。
命题 1 满足 公理 的有限子集是闭集。
命题 2 在 Hausdorff 空间中,一个序列不会收敛到两个以上的点。
- 公理:任意一点与不含它的任一闭集有不相交的(开)邻域。
- 公理:任意两个不相交的闭集有不相交的(开)邻域。
# 可数公理
# 邻域系和邻域基
设 是拓扑空间上的一点,其所有邻域组成的集合 称为点 的邻域系 (neighborhood system). 对于一个邻域系 的子集 , 若任意的邻域 , 都存在 中的元素 使得 , 则称 是点 的邻域基 (neighborhood base).
# 可数公理
可数公理 (countability axioms) 包括第一可数公理和第二可数公理,分别简称 公理和 公理。满足 公理的空间称为 空间。
第一可数公理:任一点都有可数的邻域基。
第二可数公理:空间具有可数拓扑基。满足该公理的空间称为可分空间 (separable space).
若一个空间是可分空间,则其也必定是 空间,但反之不成立。例如,
# 遗传性
若一个拓扑空间 满足性质 , 其任意子空间 都具有性质 , 则称 在 上具有遗传性 (hereditary property).
# 紧致性
# 列紧性
# 紧致度量空间
性质 对于度量空间,列紧与紧致等价。
# 紧致空间
对于一般的拓扑空间,紧致与列紧不是等价的。
# 连通性
# 定义
定义 拓扑空间 称为连通的 (connected), 若其不能分解为任意两个非空不相交开集的并。
# 道路连通性
# Ref
- 基础拓扑学讲义 尤承业
- Topological Property - Wikipedia
- Axiom of countability - Wikipedia
- Hausdorff Space - Wikipedia
- 浅谈拓扑(四) - sola 的文章 - 知乎