# 正则形式博弈

正则形式博弈 (normal-form game) 也称同时行动博弈 (simultaneous-move game) 或同时博弈 (simultaneous game), 可以用一个元组 $(N, A, u)$ 描述：

• $N=\{1,2,\dots,n\}$ 是玩家 (player) 集合；
• $A=\prod_{i=1}^nA_i$ 是所有玩家的动作向量集合，其中 $A_i$ 是玩家 $i$ 的动作 (action) 集合；
• $u=(u_1,u_2, \dots, u_n)$ 是所有玩家的效用函数 (utility function) 向量，其中 $u_i: A \to \mathbb{R}$ 是玩家 $i$ 的效用函数。

# 收益矩阵表示

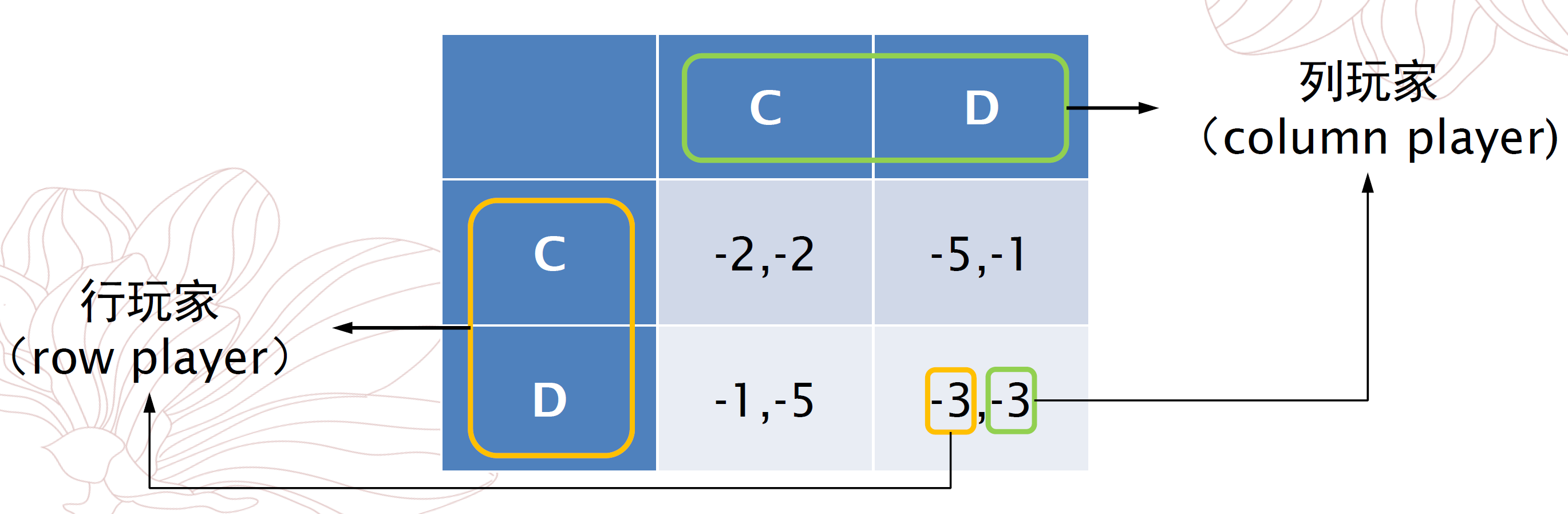
收益矩阵 (payoff matrix) 是正则形式博弈的一种常用表示方法，用于表示两个玩家的情况。对于囚徒困境，其收益矩阵如下：

在收益矩阵中，若玩家的每一选择下的结果对应一行的所有情况，则称该玩家为一个行玩家，相应地对应列的玩家称为列玩家。在收益矩阵中，一般行玩家效用写在前，列玩家效用写在后。

# 基本假设

1. 理性人假设：每个人都是理性的，即都希望最大化期望效用函数。
2. 共同知识 (common knowledge) 假设：所有玩家都指导博弈的结构 $(N, A, u)$, 所有玩家都知道所有玩家都知道博弈的结构 $(N, A, u)$ ……

# 策略

策略 (strategy) $s_i$ 是选择动作的（随机）方式，即动作集上的概率密度函数。若 $s_i(a_i)$ 是玩家 $i$ 选择动作 $a_i$ 的概率，则 $s_i(a_i)$ 满足：

$$\sum_{a_i \in A_i} s_i(a_i) = 1.$$

若存在 $a_i$ 使得 $s_i(a_i)=1$, 则称 $s_i$ 为纯策略 (pure strategy), 否则称为混合策略 (mixed strategy).

有关策略的一些常用符号包括：

• $s_{-i} = (s_1, \dots, s_{i-1}, s_{i+1}, \dots, s_n)$: 除玩家 $i$ 以外的其他玩家的策略组合。
• $\Delta(X)$: 所有定义在集合 $X$ 上的概率分布的集合。
• $\mathrm{supp}(s_i) = \{a_i|s_i(a_i)>0\}$: 支集，策略 $s_i$ 的非零概率动作集合。

# 解概念与均衡

博弈中的解是一种均衡 (equilibrium), 即没有玩家愿意改变策略。

# 纳什均衡

# 定义

若所有人都不能再提升效用，则称为均衡状态。其严谨定义如下：

若所有玩家的策略组合 (strategy profile, 也称策略剖面)

$$\bm{s}^* = (s_1^*, s_2^*, \dots, s_n^*)$$

满足

$$u_i(s_i^*, s_{-i}^*) \geq u_i(s_i, s_{-i}^*) \quad \forall s_i \in \Delta(A_i), \forall u \in N,$$

其中

$$u_i(s) = u_i(s_i, s_{-i}) = \sum_{a \in A} s(a)u_i(a) = \sum_{a \in A}u_i(a)\prod_{i \in N}s_i(a_i).$$

则称 $\bm{s}^*$ 是博弈的纳什均衡 (Nash equilibrium).

纳什均衡可以简单分类如下：

• 纯策略纳什均衡 (pure strategy Nash equilibrium): 在均衡 $s^*$ 中，每个 $s_i^*$ 都是纯策略；
• 混合策略纳什均衡 (mixed strategy Nash equilibrium): 非纯策略的纳什均衡。

# 最优回应

玩家 $i$ 对其他所有玩家策略组合 $s_{-i}$ 的最优回应 (best response) 是使得玩家 $i$ 自身效用最大的策略集合，即

$$\text{BR}_i(s_{-i}) = \argmax_{s_i \in \Delta(A_i)}u_i(s_i, s_{-i}) = \left\{s_i\left| \begin{matrix} u_i(s_i, s_{-i}) \geq u_i(s_i', s_{-i}) \\ \forall s_i' \in \Delta(A_i) \end{matrix} \right.\right\}.$$

# 优势策略

玩家 $i$ 的策略 $s_i$ 相较于 $s_i'$ 是

• 严格优势策略，若对于 $\forall s_{-i}$, 都有 $u_i(s_i, s_{-i}) > u_i(s_i', s_{-i})$.
• 弱优势策略，若对于 $\forall s_{-i}$, 都有 $u_i(s_i, s_{-i}) \geq u_i(s_i', s_{-i})$, 且存在 $s_{-i}$ 使得 $u_i(s_i, s_{-i}) > u_i(s_i', s_{-i})$.

若对于 $\forall s_i' \in \Delta(A_i)$, $s_i$ 相较于 $s_i'$ 而言都是严格（弱）优势策略，则称 $s_i$ 是一个严格（弱）优势策略。一般将弱优势策略简称为优势策略 (dominant strategy).

性质 严格优势策略或弱优势策略是唯一的，且是纯策略。

这里的唯一性显然。下面证明其是纯策略。

对于严格优势策略，若其不是纯策略，即 $|\mathrm{supp}(s_i)| > 1$, 则根据定义，$\forall a_i \in \mathrm{supp}(s_i)$ 和 $s_{-i}$, 都有 $u_i(s_i, s_{-i}) > u_i(a_i, s_{-i})$.

于是，

$$s_i(a_i) u_i(s_i, s_{-i}) > s_i(a_i) u_i(a_i, s_{-i}).$$

对支集中的所有 $a_i$ 求和，得到

$$\sum_{a_i \in \mathrm{supp}(s_i)} s_i(a_i) u_i(s_i, s_{-i}) > \sum_{a_i \in \mathrm{supp}(s_i)} s_i(a_i) u_i(a_i, s_{-i}),$$

即 $u_i(s_i, s_{-i}) > u_i(a_i, s_{-i})$, 矛盾！

对于弱优势策略，若其不是纯策略，即 $|\mathrm{supp}(s_i)| > 1$, 则根据定义，$\forall a_i \in \mathrm{supp}(s_i)$ 和 $s_{-i}$, 都有 $u_i(s_i, s_{-i}) \geq u_i(a_i, s_{-i})$, 且 $\exists s_{-i}'$ 使得 $u_i(s_i, s_{-i}') > u_i(a_i, s_{-i}')$. 仍按上述方式对支集中所有 $a_i$ 求和，得到

$$\sum_{a_i \in \mathrm{supp}(s_i)} s_i(a_i) u_i(s_i, s_{-i}) \geq \sum_{a_i \in \mathrm{supp}(s_i)} s_i(a_i) u_i(a_i, s_{-i}),$$

即 $u_i(s_i, s_{-i}) \geq u_i(a_i, s_{-i})$, 但取等号的条件是对 $\forall a_i \in \mathrm{supp}(s_i)$ 都成立，这与弱优势策略中存在严格不等号的定义相矛盾。

因此，在正则博弈中，优势策略必定是纯策略。

# 优势策略纳什均衡

若在纳什均衡 $\bm{s}^*$ 中，对于所有玩家 $i$, 都有 $s_i^*$ 是 $i$ 的严格（弱）优势策略，则称 $\bm{s}^*$ 是严格（弱）优势策略纳什均衡。

条件：

• 有限博弈 (finite game)
  • $|N|$ 有限，且 $\forall i, A_i$ 有限

性质 若某有限博弈存在严格优势策略，则该策略是纯策略的纳什均衡，且是该博弈的唯一纳什均衡。

# 纳什均衡的存在性

借助布劳尔 (Brouwer) 不动点定理。

# 极小极大策略和极大极小策略

# 极小极大策略

极小极大策略 (minimax/minmax strategy) 是一种防御策略，即选择使对手效用函数最小化的策略：

$$\argmin_{s_i}\max_{s_{-i}}u_i(s_i, s_{-i}).$$

# 极大极小策略

极大极小策略 (maximin/maxmin strategy) 是一种进攻策略，即选择使自身效用函数最大化的策略：

$$\argmax_{s_i}\min_{s_{-i}}u_i(s_i, s_{-i}).$$

# 零和博弈