# 优化问题和方法

# 优化问题

寻找某个函数 $f(x)$ 的最值的过程称为优化 (optimization). 寻找最小值和最大值可以相互转化。例如，寻找 $f(\boldsymbol{x})$ 的最大值可以转化为寻找 $-f(\boldsymbol{x})$ 的最小值。因此，我们一般认为优化问题是寻找函数最小值的问题。

此外，我们一般认为我们待求的问题不具有简单的数学求解方法，因此最优解需要通过迭代方式产生。

# 目标函数

我们将要求最值的函数 $f(\boldsymbol{x})$ 称为目标函数 (objective function) 或准则 (criterion). 将其最小化时，我们也常直接称 $f(\boldsymbol{x})$ 为代价函数 (cost function) 或损失函数 (loss function).

目标函数 $f(\boldsymbol{x})$ 可以是连续的，也可以是离散的。对于不同可微性、不同凸性的目标函数，常常采用不同的优化方法。但在这里，我们主要讨论对多元可微凸函数的优化。

# 优化方法

优化方法大致可以分为两类：确定性优化 (deterministic optimization) 和随机性优化 (stochastic optimization). 确定性优化方法中不会引入随机过程，每一步得到的结果在多次实验中都是唯一的，随机性优化则不然。梯度下降算法和牛顿法是最基本的确定性优化方法。其中，梯度下降算法只采用梯度进行优化，属于一阶优化，而牛顿法还采用 Hessian 矩阵优化，属于二阶优化方法。

# 梯度下降算法

# 基本概念

# 梯度

对于函数 $f(\bm{x})$, 衡量在点 $x$ 处的 $x_i$ 方向 $f(x)$ 如何变化的量是 $f(\bm{x})$ 在 $x_i$ 方向上的偏导数，即 $\frac{\partial}{\partial x_i}f(\bm{x})$. 我们定义梯度

$$\nabla_{\bm{x}}f(\bm{x}) := \left(\frac{\partial}{\partial x_1}f(\bm{x}), \frac{\partial}{\partial x_2}f(\bm{x}), \dots, \frac{\partial}{\partial x_n}f(\bm{x})\right) = \sum_{i=1}^n\frac{\partial}{\partial x_i}f(\bm{x}) \frac{x_i}{\|x_i\|}.$$

# 方向导数

我们定义向量 $u$ 方向上的方向导数 (directional derivative) 为

$$\frac{\partial}{\partial \alpha}f(x + \alpha u).$$

于是根据梯度的定义，有

$$\frac{\partial}{\partial \alpha}f(x + \alpha u) = u^\top \nabla_xf(x).$$

# 梯度下降算法推导

# 启发式的推导

我们假设 $f$ 是一个恒正的函数。为快速寻找 $f$ 在定义域上的最小值，对一个初始点 $\bm{x}$, 我们希望找到 $\bm{x}$ 处使 $f$ 下降最快的方向，即寻找

$$\min_{\bm{u}, |\bm{u}| = 1}u^\top \nabla_{\bm{x}} f(\bm{x}).$$

我们有

$$\min_{\bm{u}, |\bm{u}| = 1}\bm{u}^\top \nabla_{\bm{x}} f(\bm{x}) = \min_{\bm{u}, \|\bm{u}\| = 1}\|\nabla_{\bm{x}} f(\bm{x})\|_2\cos \theta,$$

其中 $\theta$ 是 $\bm{u}$ 与 $\nabla_{\bm{x}} f(\bm{x})$ 的夹角。

显然，$\bm{u}$ 与 $\nabla_{\bm{x}} f(\bm{x})$ 反向时，该值最小。于是我们只需计算函数 $f$ 在点 $\bm{x}$ 处的梯度，在负梯度上移动可以最快达到最小值。这种方法被称为梯度下降算法 (gradient descent algorithm).

根据梯度下降算法，我们每次迭代得到的新的点为

$$x' = x - \alpha \nabla_x f(x),$$

其中 $\alpha$ 称为学习率 (learning rate) 或步长。上式称为更新方程。当算法迭代至一定次数后，有 $\nabla_x f(x) \to 0$, 此时我们取一个临界值，当 $\nabla_x f(x)$ 小于临界值时，认为算法结束。

# 正经一点的推导

首先，我们给出采样点 $\bm{x}_t$ 附近函数值的估计：

$$f(\bm{x}) \approx f(\bm{x}_t) + \nabla f(\bm{x}_t)^T(\bm{x}-\bm{x}_t) + \frac{1}{2\eta_t}\|\bm{x}-\bm{x}_t\|^2.$$

其中，正则项是 $\frac{1}{2\eta_t}\|\bm{x}-\bm{x}_t\|^2$, 起到了限制 $\bm{x}$ 与 $\bm{x}_t$ 之间距离的作用，$\eta_t$ 越大，则意味着正则项的影响越弱，对距离的限制越少。

在优化问题中，我们希望找到一个 $\bm{x}$ 使得 $f(\bm{x})$ 最小化。为了找到这个 $\bm{x}$, 我们需要求解一个包含正则项的优化问题，即

$$\min_{\bm{x}} \left( f(\bm{x}_t) + \nabla f(\bm{x}_t)^T(\bm{x}-\bm{x}_t) + \frac{1}{2\eta_t}\|\bm{x}-\bm{x}_t\|^2 \right)$$

这个优化问题的解可以通过求导并令导数为零来找到。具体来说，我们对 $\bm{x}$ 求导：

$$\nabla_{\bm{x}} \left( f(\bm{x}_t) + \nabla f(\bm{x}_t)^T(\bm{x}-\bm{x}_t) + \frac{1}{2\eta_t}\|\bm{x}-\bm{x}_t\|^2 \right) = \nabla f(\bm{x}_t) + \frac{1}{\eta_t}(\bm{x}-\bm{x}_t).$$

令导数为零，我们得到：

$$\nabla f(\bm{x}_t) + \frac{1}{\eta_t}(\bm{x}-\bm{x}_t) = 0$$

解方程得到：

$$\bm{x} = \bm{x}_t - \eta_t \nabla f(\bm{x}_t)$$

这就是梯度下降法的参数更新公式。

# 梯度下降算法的问题和优化

这部分内容不仅是梯度下降算法存在的问题，也是诸多迭代优化算法中需要面对的问题。其解决思路也与梯度下降算法相似。

# 大样本下的效率问题

面对大规模的样本，仍然采用朴素的梯度下降方法会存在两个问题，一是训练样本无法完全装入内存，二是单次训练所需时间过长。

# 随机梯度下降

为了解决大样本下的训练效率问题，随机梯度下降 (Stochastic Gradient Decent, SGD) 采用在样本中再次随机取样的方式进行训练。SGD 的一个改进为 mini-batch SGD, 即小批量随机梯度下降。其每次在样本中随机选择一定数量的样本作为一个批次 (batch), 执行一次梯度更新。

mini-batch SGD 算法包括以下步骤 (朴素 SGD 只需要取 $m=1$)：

1. 从训练集中随机选出 $m$ 项 $\{\boldsymbol{x}^{(1)}, \boldsymbol{x}^{(2)}, \dots, \boldsymbol{x}^{(n)}\}$, 及其对应标签 $y^{(i)}$.
2. 求梯度

$$\hat{\boldsymbol{g}} \leftarrow +\frac{1}{m}\nabla_{\boldsymbol{\theta}}\sum_i L(f(\boldsymbol{x}^{(i)}; \boldsymbol{\theta}), \boldsymbol{\theta}, y^{(i)})$$

3. 更新解

$$\boldsymbol{\theta} \leftarrow \boldsymbol{\theta} - \alpha\hat{\boldsymbol{g}}$$

4. 判断是否满足停机条件，否则跳回 1.

注意到，由于单次只选取一个样本，造成 SGD 的一个缺点是容易陷入局部最优解。

# 训练速度和精度问题

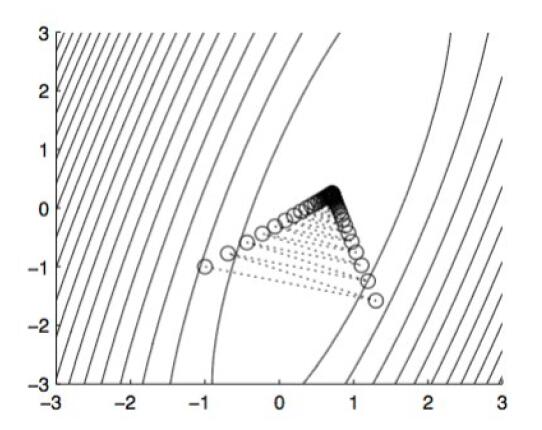
先前介绍的朴素梯度下降算法和 SGD 中，学习率都是一个确定的超参数。学习率的优劣，会极大程度上影响训练的速度和精度。学习率过低时，梯度下降过程缓慢，需要的迭代次数较多，但最终可以到达的最优解较精确；学习率过高时，尽管训练速度快，但在接近最优解时会出现较强的震荡现象，(我们称为 zig-zagging 问题) 得到的最优解不精确。

面对这种情况，目前主要的解决思路有两种。分别是基于动量的梯度下降和自适应学习率的梯度下降。

# 动量梯度下降法

经典的动量梯度下降法 (Polyak's Classical Momentum) 由 Polyak 于 1964 年提出。动量梯度下降的更新方程如下：

$$\begin{aligned} & \boldsymbol{\theta}_{t+1} = \boldsymbol{\theta}_t + \boldsymbol{v}_{t+1} \\ & \boldsymbol{v}_{t+1} = \mu \boldsymbol{v}_t - \eta \nabla_{\boldsymbol{\theta}_t}f \end{aligned}$$

也就是说，其以速度矢量 (velocity vector) $\boldsymbol{v}$ 取代了更新所用的梯度。速度矢量包含了对先前梯度的记忆，记忆是指数衰减的，其衰减系数 $\mu \in [0,1]$.

# Nesterov Accelerated Gradient (NAG) 算法

是 Polyak 的经典动量梯度方法的改进，于 1981 年提出，其思想类似数值分析中的 Runge-Kutta 方法，采用计算提前量的方式使估计更精细。其具体的更新规则如下：

$$\begin{aligned} & \boldsymbol{\theta}_{t+1} = \boldsymbol{\theta}_t + \boldsymbol{v}_{t+1} \\ & \boldsymbol{v}_{t+1} = \mu \boldsymbol{v}_t - \eta \nabla_{\boldsymbol{\theta}_t+\mu \boldsymbol{v}_t}f \end{aligned}$$

# AdaGrad

除了采用动量梯度下降的方式外，另一种调整方式是实现自适应的学习率调整。AdaGrad (Adaptive Gradient Algorithm, 2011) 是其中最基础的一种方式。其核心是采用累积梯度平方实现各参数学习率的自适应下降。其更新方程为：

$$\begin{aligned} & \boldsymbol{g}_t = \nabla_{\boldsymbol{\theta}_t}f\\ & G_t=\sum_{\tau=1}^t\boldsymbol{g}_{\tau}\boldsymbol{g}_{\tau}^\top\\ & \theta_{t+1,i} = \theta_{t,i} - \frac{\eta}{\sqrt{G_{t,ii}+\varepsilon}} g_{t,i}\\ \end{aligned}$$

其中， $i$ 为参数下标， $t$ 为更新步数 (time)， $G_t$ 是 $t$ 时刻对全体更新过程的梯度外积求和得到的矩阵，对角元素表示对应参数分量的全过程梯度平方和。

这样做存在的一个缺点是，训练后期的 $G_t$ 较大，更新步长太小，导致模型的收敛速度慢。

# RMSProp

均方根传播算法 (Root Mean Square Propagation, RMSProp) 也是一种对每个参数自适应学习率的梯度下降算法。其结合了动量梯度下降和 AdaGrad 算法的思想，更新方程如下：

$$\begin{aligned} & \boldsymbol{g}_t = \nabla_{\boldsymbol{\theta}_t}f \\ & G_t=\boldsymbol{g}_{t}\boldsymbol{g}_{t}^\top\\ & v_{t+1,i} = \gamma v_{t,i} + (1-\gamma) G_{t,ii}\\ & \theta_{t+1,i} = \theta_{t,i} - \frac{\eta}{\sqrt{v_{t,i}+\varepsilon}}g_{t,i} \end{aligned}$$

# Adam

# Reference

• 参考
• 一文看懂常用的梯度下降算法